Πείραμα: Μέτρηση της επιφανειακής τάσης με κέρματα!

Αφού η πολιτική των κυβερνήσεων και των τραπεζών όλου του κόσμου είναι η κατάργηση των μετρητών, άρα και των κερμάτων, καλό είναι να κάνετε τα πειράματα που περιγράφονται στη συνέχεια όσο το δυνατόν συντομότερα.
Μια από τις συνέπειες της κατάργησης των κερμάτων, θα είναι και η δυσκολία της εύρεσης «καθημερινών» υλικών για την πραγματοποίηση απλών πειραμάτων φυσικής.
Μάλλον όμως αυτό είναι το μικρότερο κακό. Γιατί διαβάζοντας κανείς το βιβλίο του Γερμανού δημοσιογράφου Norbert Häring με τίτλο «Η κατάργηση των μετρητών και οι συνέπειες της» , διαπιστώνει πράγματα που μάλλον δεν είχε συνειδητοποιήσει, υπνωτισμένος από την ευκολία που προσφέρουν (προς το παρόν) οι τραπεζικές κάρτες και το e-banking.
Ας δούμε λοιπόν, όσο είναι ακόμα καιρός, δυο όμορφα πειράματα φυσικής με «μετρητά» που σήμερα βρίσκονται εύκολα ανά πάσα στιγμή.

Πότε είναι πραγματικά γεμάτο ένα κύπελλο με νερό;

Προσπαθήστε να απαντήσετε στο ερώτημα αυτό κάνοντας το εξής πείραμα: Γεμίστε ένα κύπελλο με νερό ώσπου να σας φανεί ότι αποκλείεται να χωρέσει έστω και μια σταγόνα ακόμη.
Στη συνέχεια, αρχίστε να προσθέτετε δεκάλεπτα στο κύπελλο, ακουμπώντας τα ένα ένα απαλά στο νερό, με το πλάι, και αφήνοντάς τα να βυθιστούν. Θα διαπιστώσετε ότι θα χρειαστεί να προσθέσετε αρκετά δεκάλεπτα ώσπου το νερό να φτάσει να ξεχειλίσει. Το κύπελλο δεν ήταν τελικά τόσο γεμάτο όσο νομίζαμε στην αρχή.

Πείραμα 1

Πάρτε ένα πλαστικό κύπελλο και γεμίστε το με νερό ώσπου η επιφάνειά του να βρεθεί στο ίδιο επίπεδο με τα χείλη του κυπέλλου. Προσθέστε κατόπιν με μεγάλη προσοχή δεκάλεπτα, έτσι όπως περιγράψαμε παραπάνω, ώσπου το νερό να ξεχειλίσει. Τέλος, καταγράψτε το πλήθος των δεκάλεπτων που προσθέσατε.

          

Φανταστείτε το νερό ως αποτελούμενο από ένα ασύλληπτα μεγάλο πλήθος μικροσκοπικών μορίων. Επιπλέον, φανταστείτε το κάθε μόριο του νερού να έλκεται έντονα από τα γειτονικά του μόρια. Συνεπώς, τα μόρια υπάρχουν ως ένα διασυνδεόμενο δίκτυο, και όχι ως μεμονωμένα, ανεξάρτητα σωματίδια. Μάλιστα, ανάμεσα στα μόρια του νερού αναπτύσσονται τόσο ισχυρές έλξεις ώστε η υδάτινη επιφάνεια τείνει να απωθεί κάθε τι που προσπαθεί να εισχωρήσει στο δίκτυο.
Κάθε μόριο νερού στο εσωτερικό αυτού του δικτύου υφίσταται ισχυρές διαμοριακές έλξεις προς όλες τις κατευθύνσεις, όπως φαίνεται στο παρακάτω σχήμα

Οι διαμοριακές έλξεις στην επιφάνεια και στο εσωτερικό ενός υγρού.

Ωστόσο, η κατάσταση διαφοροποιείται σημαντικά εφόσον πρόκειται για τα μόρια της επιφάνειας. Αυτά έλκονται μόνο από τα γειτονικά τους επιφανειακά μόρια και από όσα μόρια βρίσκονται κάτω από την επιφάνεια. Ως εκ τούτου, πάνω τους ασκείται μια συνισταμένη προς τα έσω δύναμη, η οποία έχει ως αποτέλεσμα την εμφάνιση επιφανειακής τάσης, ή, για να περιγράψουμε τα πράγματα πιο παραστατικά, το σχηματισμό μιας λεπτής «επιδερμίδας» που καλύπτει τον κύριο όγκο του νερού.
Ο συντελεστής επιφανειακής τάσης ενός υγρού ορίζεται τυπικά ως το απαιτούμενο έργο για την αύξηση του εμβαδού της επιφάνειάς του κατά μία μονάδα. Εναλλακτικά, αν θεωρήσουμε ένα ευθύγραμμο τμήμα το οποίο μετατοπίζεται κατά την κάθετη προς αυτό κατεύθυνση έτσι ώστε να αυξηθεί το εμβαδόν της επιφάνειας του υγρού, μπορούμε να εννοήσουμε το συντελεστή επιφανειακής τάσης ανά μονάδα μήκους δύναμη που ανθίσταται στη μετατόπιση του ευθυγράμμου τμήματος.
Όσο μεγαλύτερη έλξη ασκεί το ένα μόριο του υγρού στο άλλο τόσο μεγαλύτερος είναι ο συντελεστής επιφανειακής τάσης του υγρού. Τα μόρια του νερού θα κάνουν σχεδόν τα πάντα για να αποτρέψουν την απόσπαση ενός ή περισσότερων μορίων από την επιφάνεια. Άλλα υγρά, φυσικά, χαρακτηρίζονται από διαφορετικούς συντελεστές επιφανειακής τάσης, οι οποίοι και χρησιμεύουν ως μέτρο των έλξεων που αναπτύσσονται μεταξύ των μορίων του υγρού.

Πείραμα 2

Γεμίστε ένα πλαστικό κύπελλο με ισοπροπυλική αλκοόλη[1] ώσπου η επιφάνεια του υγρού να φτάσει στο ίδιο επίπεδο με τα χείλη του κυπέλλου. Όπως και στο πείραμα 1, προσθέστε δεκάλεπτα προσεκτικά, ώσπου τελικά το κύπελλο να ξεχειλίσει. Συγκρίνετε το πλήθος των δεκαλέπτων που χρησιμοποιήσατε τούτη τη φορά με το αντίστοιχο πλήθος στην περίπτωση του νερού.
Ετοιμάστε τώρα λίγο αλατόνερο διαλύοντας 40 g αλατιού (δυο κουταλιές της σούπας) επιτραπέζιο αλάτι σε 160 cm3 νερού. Γεμίστε ένα άλλο πλαστικό κύπελλο με αυτό το διάλυμα – η επιφάνειά του να ανεβεί ως τα χείλη του κυπέλλου. Προσθέστε και πάλι δεκάλεπτα, ώσπου το διάλυμα να ξεχειλίσει, και καταγράψτε το πλήθος των δεκαλέπτων που χρησιμοποιήσατε.
Παρατηρήστε πόσο έντονα φουσκώνει το υγρό πάνω από τα χείλη του κυπέλλου σε καθένα από αυτά τα τρία συστήματα (νερό, ισοπροπυλική αλκοόλη και αλατόνερο). Όσο μεγαλύτερο συντελεστή επιφανειακής τάσης έχει το υγρό τόσο εντονότερα φουσκώνει και τόσο περισσότερα δεκάλεπτα μπορεί να χωρέσει χωρίς να ξεχειλίσει.

Προσθέστε μια σταγόνα υγρού απορρυπαντικού στο γεμάτο κέρματα κύπελλο του πρώτου πειράματος. Τι παρατηρείτε;

Μπορείτε να κάνετε μια χονδρική βαθμονόμηση του συντελεστή επιφανειακής τάσης γ του υγρού βάσει του πλήθους των δεκαλέπτων που χρειάζονται ώστε να ξεχειλίσει το κύπελλο. Προς τούτο, δεν έχετε παρά να παραστήσετε γραφικά την τιμή του συντελεστή επιφανειακής τάσης (από τον παρακάτω πίνακα που θα τον συμπληρώσετε βάσει των πειραματικών αποτελεσμάτων σας) συναρτήσει του πλήθους των κερμάτων τα οποία προσθέσατε στο κύπελλο ώσπου να ξεχειλίσει.
                                      

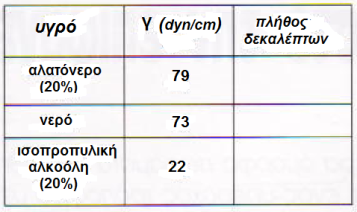
Οι τιμές του συντελεστή επιφανειακής τάσης των υγρών που περιέχονται στην δεύτερη στήλη αντιστοιχούν σε θερμοκρασία 20 βαθμών Κελσίου
Είναι γραμμική η σχέση που προκύπτει; Αφού ετοιμάσετε ποικίλα διαλύματα ισοπροπυλικής αλκοόλης και νερού, μετρήστε τους συντελεστές επιφανειακής τάσης στηριζόμενοι στο πλήθος των δεκαλέπτων που απαιτούνται για να ξεχειλίσουν τα αντίστοιχα κύπελλα. Προσδιορίστε κατά πόσον ο συντελεστής επιφανειακής τάσης συνιστά ή όχι γραμμική συνάρτηση της συγκέντρωσης.
Τέλος, μετρήστε τους συντελεστές επιφανειακής τάσης άλλων υγρών (για παράδειγμα, διαλυμάτων ξιδιού και σαπουνιού) που έχετε διαθέσιμα στην κουζίνα του σπιτιού σας.
Γιατί διαφέρουν οι συντελεστές επιφανειακής τάσης της ισοπροπυλικής αλκοόλης και του αλατόνερου από εκείνον του καθαρού νερού;
Πως επιδρά το απορρυπαντικό στον συντελεστή επιφανειακής τάσης του νερού;
Μήπως έτσι εξηγούνται ορισμένες ιδιότητες των απορρυπαντικών οι οποίες τα καθιστούν κατάλληλα για το πλύσιμο των ρούχων;
Κατά μια έννοια, μπορούμε να θεωρήσουμε ότι τα μόρια ενός υγρού είναι συγκολλημένα το ένα με το άλλο με κάποιου είδους μοριακή «κόλλα». Ένα υγρό όπως η ισοπροπυλική αλκοόλη έχει πολύ ασθενέστερη «κόλλα» απ’ ότι το νερό, γεγονός που καθιστά ευκολότερη τη διείσδυση δια της επιφανείας του.
Μια και τα μόρια που συγκροτούν την επιφάνεια κολλούν μεταξύ τους, δεν δυσκολευόμαστε να αντιληφθούμε γιατί η επιφάνεια του υγρού ανθίσταται στις διεισδύσεις.
Η επιφανειακή τάση του νερού διαδραμάτισε κεντρικό ρόλο στην εξέλιξη της υδρόβιας ζωής, δεδομένου ότι το υπολειμματικό υλικό που επικάθεται στις επιφάνειες των νερόλακκων παρέχει καταφύγιο και τροφή σε ποικίλους οργανισμούς. Επιπλέον, ο υψηλός συντελεστής επιφανειακής τάσης του νερού επιτρέπει σε ορισμένα έντομα να βαδίζουν πάνω στην επιφάνειά του. Μολονότι τα έντομα έχουν μεγαλύτερη πυκνότητα από το νερό, εντούτοις, όταν το βάρος τους κατανέμεται κατά μήκος των απλωμένων άκρων τους, δεν ασκεί πίεση ικανή να υπερισχύσει της επιφανειακής τάσης του νερού.

Κέρματα που επιπλέουν και έλκονται μεταξύ τους

Στα προηγούμενα πειράματα βυθίζαμε τα κέρματα αργά και σταθερά με το πλάι. Στο βίντεο που ακολουθεί τα κέρματα τοποθετούνται αργά και σταθερά με την μεγάλη επιφάνειά τους στο νερό, έτσι ώστε να επιπλέουν! Παρατηρήστε ότι τα κέρματα αφού επιπλεύσουν έλκονται μεταξύ τους. Στη συνέχεια προστίθενται στο νερό μερικές σταγόνες απορρυπαντικού. Δείτε τι θα συμβεί:

            

Πηγή: «Παρατηρήστε την επιφανειακή τάση», Mary E. Stokes και Henry D. Screiber, περιοδικό QUANTUM, Τόμος 8 / Τεύχος 4 (Ιούλιος/Αύγουστος 2001)

https://physicsgg.me/

[1] Την ισοπροπυλική αλκοόλη μπορείτε να την προμηθευτείτε από τα περισσότερα φαρμακεία υπό μορφή διαλύματος 91%. Για να προστατέψετε την επιφάνεια του τραπεζιού από τα υγρά που θα ξεχειλίσουν, συνιστάται να τοποθετήσετε κάτω από κάθε κύπελλο ένα πιάτο.