Τι είναι ένα στοιχειώδες σωματίδιο;
Μια απλή απάντηση, ότι δηλαδή: τα ηλεκτρόνια, τα φωτόνια, τα κουάρκ και άλλα «στοιχειώδη» σωματίδια δεν έχουν δομή ή φυσική έκταση, φαίνεται εκ των πραγμάτων μη ικανοποιητική. Σύμφωνα με την Mary Gaillard, που προέβλεψε τις μάζες δυο τύπων κουάρκ στην δεκαετία του 1970, «βασικά πιστεύουμε ότι ένα σωματίδιο είναι ένα σημειακό αντικείμενο». Ωστόσο τα σωματίδια έχουν διακριτά χαρακτηριστικά, όπως φορτίο και μάζα. Πώς μπορεί ένα σημείο χωρίς διαστάσεις να έχει βάρος;
Λέμε ότι είναι «στοιχειώδη», λέει ο Xiao-Gang Wen, θεωρητικός φυσικός στο Τεχνολογικό Ινστιτούτο της Μασαχουσέτης. Αλλά αυτός είναι απλώς ένας [τρόπος για να πεις] στους φοιτητές, «Μην ρωτάτε! Δεν ξέρω την απάντηση. Είναι στοιχειώδη, μην ξαναρωτήσετε».
Για οποιοδήποτε άλλο αντικείμενο, οι ιδιότητες του αντικειμένου εξαρτώνται από τη φυσική του σύνθεση – και τελικά, από τα συστατικά του σωματίδια. Όμως οι ιδιότητες αυτών των σωματιδίων δεν προέρχονται από συστατικά τους αλλά από μαθηματικά πρότυπα. Ως σημεία επαφής μεταξύ μαθηματικών και πραγματικότητας, τα σωματίδια εκτείνονται και στους δύο κόσμους σε μια αβέβαιη βάση.
Όταν ρώτησα πρόσφατα δώδεκα φυσικούς σωματιδίων «τι είναι ένα σωματίδιο;», έδωσαν εντελώς διαφορετικές περιγραφές. Τόνισαν ότι οι απαντήσεις τους δεν έρχονται σε σύγκρουση, αλλά καταγράφουν διαφορετικές πτυχές της αλήθειας. Περιέγραψαν επίσης δύο πρόσφατες σημαντικές ερευνητικές ιδέες στη θεμελιώδη φυσική οι οποίες επιδιώκουν μια πιο ικανοποιητική και ολοκληρωμένη εικόνα των σωματιδίων.
«Τι είναι ένα σωματίδιο;» είναι πράγματι μια πολύ ενδιαφέρουσα ερώτηση, λέει ο Wen.»Σήμερα υπάρχει πρόοδος όσον αφορά την απάντηση. Δεν πρέπει να πω ότι υπάρχει μια ενιαία άποψη, αλλά υπάρχουν πολλές διαφορετικές απόψεις και όλες φαίνονται ενδιαφέρουσες.»
Σωματίδιο είναι μια «κατάρρευση κυματοσυνάρτησης»
“Την στιγμή που το ανιχνεύω, καταρρέει η κυματοσυνάρτηση και γίνεται σωματίδιο… [Το σωματίδιο είναι] η κυματοσυνάρτηση που κατέρρευσε».
—Δημήτρης Νανόπουλος
Ο προβληματισμός για κατανόηση των θεμελιωδών δομικών στοιχείων της φύσης ξεκίνησε με τον ισχυρισμό του αρχαίου Έλληνα φιλόσοφου Δημόκριτου περί ατόμων. Δύο χιλιετίες μετά, ο Isaac Newton και ο Christiaan Huygens διαφώνησαν για το αν το φως συνίσταται από σωματίδια ή κύματα. Η ανακάλυψη της κβαντικής μηχανικής μετά από περίπου 250 χρόνια απέδειξε πως και οι δυο αυθεντίες είχαν δίκιο: Το φως συνίσταται από πακέτα ενέργειας γνωστά ως φωτόνια, τα οποία συμπεριφέρονται τόσο ως σωματίδια όσο και ως κύματα.
Η δυαδικότητα των κυμάτων-σωματιδίων κατέληξε να είναι ένα σύμπτωμα μιας βαθύτερης σπανιότητας. Η κβαντομηχανική αποκάλυψε στους θεμελιωτές της την δεκαετία του 1920 ότι τα φωτόνια και άλλα κβαντικά αντικείμενα περιγράφονται καλύτερα όχι ως σωματίδια ή κύματα αλλά από αφηρημένες «κυματοσυναρτήσεις» – εξελισσόμενες μαθηματικές συναρτήσεις που δείχνουν την πιθανότητα ενός σωματιδίου να έχει διάφορες ιδιότητες. Για παράδειγμα, η κυματοσυνάρτηση που αντιπροσωπεύει ένα ηλεκτρόνιο απλώνεται χωρικά, έτσι ώστε το ηλεκτρόνιο να έχει πιθανές θέσεις και όχι μια συγκεκριμένη. Αλλά κατά κάποιο παράξενο τρόπο, όταν χρησιμοποιείτε έναν ανιχνευτή για να προσδιορίσετε την θέση του ηλεκτρονίου, η κυματοσυνάρτηση ξαφνικά «καταρρέει» σε ένα σημείο και το σωματίδιο κάνει κλικ σε αυτήν τη θέση στον ανιχνευτή.
Η δυαδικότητα των κυμάτων-σωματιδίων κατέληξε να είναι ένα σύμπτωμα μιας βαθύτερης σπανιότητας. Η κβαντομηχανική αποκάλυψε στους θεμελιωτές της την δεκαετία του 1920 ότι τα φωτόνια και άλλα κβαντικά αντικείμενα περιγράφονται καλύτερα όχι ως σωματίδια ή κύματα αλλά από αφηρημένες «κυματοσυναρτήσεις» – εξελισσόμενες μαθηματικές συναρτήσεις που δείχνουν την πιθανότητα ενός σωματιδίου να έχει διάφορες ιδιότητες. Για παράδειγμα, η κυματοσυνάρτηση που αντιπροσωπεύει ένα ηλεκτρόνιο απλώνεται χωρικά, έτσι ώστε το ηλεκτρόνιο να έχει πιθανές θέσεις και όχι μια συγκεκριμένη. Αλλά κατά κάποιο παράξενο τρόπο, όταν χρησιμοποιείτε έναν ανιχνευτή για να προσδιορίσετε την θέση του ηλεκτρονίου, η κυματοσυνάρτηση ξαφνικά «καταρρέει» σε ένα σημείο και το σωματίδιο κάνει κλικ σε αυτήν τη θέση στον ανιχνευτή.
Ένα σωματίδιο είναι μια κυματοσυνάρτηση που κατέρρευσε. Αλλά τι σημαίνει αυτό στον κόσμο; Γιατί η παρατήρηση προκαλεί την κατάρρευση μιας «απλωμένης» μαθηματικής συνάρτησης και την εμφάνιση ενός συγκεκριμένου σωματιδίου; Και ποιός αποφασίζει το αποτέλεσμα της μέτρησης; Εδώ και σχεδόν έναν αιώνα, οι φυσικοί δεν έχουν ιδέα.
Σωματίδιο είναι μια ‘Κβαντική Διέγερση ενός Πεδίου’
«Τι είναι ένα σωματίδιο για έναν φυσικό; Είναι μια κβαντική διέγερση ενός πεδίου. Γράφουμε την φυσική σωματιδίων σε μια μαθηματική γλώσσα που ονομάζεται κβαντική θεωρία πεδίου. Δεδομένου ότι υπάρχουν πολλά διαφορετικά πεδία, με κάθε πεδίο να έχει διαφορετικές ιδιότητες και διαφορετικές διεγέρσεις ανάλογα με τις ιδιότητες, αυτές τις διεγέρσεις μπορούμε να τις θεωρήσουμε ως σωματίδια.»
—Helen Quinn
Στη δεκαετία του 1930 η εικόνα έγινε ακόμη πιο παράξενη. Οι φυσικοί συνειδητοποίησαν ότι οι κυματοσυναρτήσεις πολλών μεμονωμένων φωτονίων συμπεριφέρονται συλλογικά σαν ένα μόνο κύμα που διαδίδεται μέσω σύμφωνων ηλεκτρικών και μαγνητικών πεδίων – ακριβώς όπως η κλασική εικόνα του φωτός που ανακαλύφθηκε τον 19ο αιώνα από τον James Clerk Maxwell. Αυτοί οι ερευνητές διαπίστωσαν ότι θα μπορούσαν να «κβαντώσουν» την κλασική θεωρία πεδίων, περιορίζοντας τα πεδία, ώστε να μπορούν να ταλαντώνονται μόνο σε διακριτές ποσότητες γνωστές ως «κβάντα» των πεδίων. Εκτός από τα φωτόνια – τα κβάντα του φωτός – ο Paul Dirac και άλλοι ανακάλυψαν ότι η ιδέα θα μπορούσε να επεκταθεί σε ηλεκτρόνια και σε οτιδήποτε άλλο: Σύμφωνα με την κβαντική θεωρία πεδίου, τα σωματίδια είναι διεγέρσεις των κβαντικών πεδίων που γεμίζουν όλο το χώρο.
Θεωρώντας την ύπαρξη αυτών των πιο θεμελιωδών πεδίων, η κβαντική θεωρία πεδίου απογύμνωσε την κατάσταση των σωματιδίων, χαρακτηρίζοντάς τα ως απλά μπιτ ενέργειας που θέτουν τα πεδία σε «παφλασμό». Ωστόσο, παρά το οντολογικό φορτίο των πανταχού παρόντων πεδίων, η κβαντική θεωρία πεδίου έγινε η κοινή γλώσσα της σωματιδιακής φυσικής, επειδή επιτρέπει στους ερευνητές να υπολογίζουν με ακρίβεια τι συμβαίνει όταν αλληλεπιδρούν σωματίδια – οι αλληλεπιδράσεις σωματιδίων είναι, σε βασικό επίπεδο, ο τρόπος με τον οποίο ο κόσμος συναρμολογείται.
Καθώς οι φυσικοί ανακάλυπταν όλο και περισσότερα σωματίδια και τα σχετικά πεδία τους, αναπτύχθηκε μια παράλληλη προοπτική. Οι ιδιότητες αυτών των σωματιδίων και πεδίων φαίνονταν να ακολουθούν αριθμητικά μοτίβα. Επεκτείνοντας αυτά τα μοτίβα, οι φυσικοί μπόρεσαν να προβλέψουν την ύπαρξη περισσότερων σωματιδίων. «Άπαξ και κωδικοποιήσετε τα μοτίβα που παρατηρείτε στα μαθηματικά, τα μαθηματικά διαθέτουν προβλεπτικότητα. Σου λένε περισσότερα πράγματα από αυτά που μπορείς να παρατηρήσεις, επισημαίνει η Helen Quinn, φυσικός σωματιδίων στο Πανεπιστήμιο του Στάνφορντ.
Τα μοτίβα υποδεικνύουν επίσης μια πιο αφηρημένη και ενδεχομένως βαθύτερη οπτική για το τι είναι στ’ αλήθεια τα σωματίδια.
Ένα σωματίδιο είναι μια «μη-αναγώγιμη αναπαράσταση ομάδας»
«Τα σωματίδια περιγράφονται στο ελάχιστο από μη αναγώγιμες αναπαραστάσεις της ομάδας Poincaré.»
— Sheldon Glashow
Ο Mark Van Raamsdonk θυμάται το ξεκίνημα του πρώτου μαθήματος της κβαντικής θεωρίας πεδίου, ως μεταπτυχιακός φοιτητής στο Πανεπιστήμιο του Πρίνστον. Ο καθηγητής μπήκε στην αίθουσα, κοίταξε τους μαθητές και ρώτησε: «Τι είναι ένα σωματίδιο;»
«Μια μη αναγωγίσιμη αναπαράσταση της ομάδας Poincaré», απάντησε ένας διαβασμένος συμφοιτητής.
Λαμβάνοντας τον προφανώς σωστό ορισμό ως γενική γνώση, ο καθηγητής παρέλειψε οποιαδήποτε εξήγηση και άρχισε μια ακατανόητη σειρά διαλέξεων. «Όλο αυτό το εξάμηνο δεν έμαθα τίποτα από το μάθημα», δήλωσε ο Van Raamsdonk, ο οποίος είναι πλέον ένας αναγνωρισμένος θεωρητικός φυσικός στο Πανεπιστήμιο του Βανκούβερ.
Είναι μια βαθύτερη συνηθισμένη απάντηση των ανθρώπων που γνωρίζουν: Τα σωματίδια είναι «αναπαραστάσεις» των «ομάδων συμμετρίας», οι οποίες είναι σύνολα μετασχηματισμών που μπορούν να εφαρμοστούν σε αντικείμενα.
Πάρτε, για παράδειγμα, ένα ισόπλευρο τρίγωνο. Περιστρέφοντάς το κατά 120 ή 240 μοίρες, ή ανακλώντας ως προς την ευθεία που διέρχεται από κάποιο ύψος του, ή μη κάνοντας τίποτα, όλα αφήνουν το τρίγωνο αναλλοίωτο να φαίνεται όπως ήταν πριν. Αυτές οι έξι συμμετρίες σχηματίζουν μια ομάδα. Η ομάδα μπορεί να εκφραστεί ως ένα σύνολο μαθηματικών πινάκων – διατάξεις αριθμών που, όταν πολλαπλασιαστούν με τις συντεταγμένες ισόπλευρου τριγώνου, δίνουν τις ίδιες συντεταγμένες. Ένα τέτοιο σύνολο πινάκων είναι μια «αναπαράσταση» της ομάδας συμμετρίας.
Με παρόμοιο τρόπο, τα ηλεκτρόνια, τα φωτόνια και άλλα στοιχειώδη σωματίδια είναι αντικείμενα που ουσιαστικά παραμένουν τα ίδια όταν δρα σ’ αυτά μια συγκεκριμένη ομάδα. Δηλαδή, τα σωματίδια είναι αναπαραστάσεις της ομάδας Poincaré: η ομάδα των 10 (μετασχηματισμών) τρόπων μετακίνησης στο χωροχρονικό συνεχές. Τα αντικείμενα μπορούν να μετακινηθούν σε τρεις χωρικές κατευθύνσεις ή να μετατοπιστούν χρονικά. Μπορούν επίσης να περιστραφούν σε τρεις κατευθύνσεις ή να αποκτήσουν ορμή σε οποιαδήποτε από αυτές τις κατευθύνσεις. Το 1939, ο φυσικο-μαθηματικός Eugene Wigner όρισε τα σωματίδια ως τα απλούστερα δυνατά αντικείμενα που μπορούν να μετατοπιστούν, να περιστραφούν και να ωθηθούν.
Για να μετασχηματιστεί σωστά ένα αντικείμενο κάτω από αυτούς τους 10 μετασχηματισμούς Poincaré, συνειδητοποίησε ότι πρέπει να έχει ένα ορισμένο ελάχιστο σύνολο ιδιοτήτων και τα σωματίδια να έχουν αυτές τις ιδιότητες. H μια είναι η ενέργεια. Κατά βάθος, η ενέργεια είναι απλά η ιδιότητα που παραμένει ίδια όταν το αντικείμενο μετατοπίζεται χρονικά. Η ορμή είναι η ιδιότητα που παραμένει ίδια όταν το αντικείμενο μετατοπίζεται στον χώρο.
Μια τρίτη ιδιότητα απαιτείται για τον προσδιορισμό του τρόπου με τον οποίο τα σωματίδια αλλάζουν κάτω από τον συνδυασμό μετασχηματισμών χωρικών περιστροφών και μετατοπίσεων (που, μαζί, είναι περιστροφές στο χωροχρόνο). Αυτή η ιδιότητα-κλειδί είναι το «σπιν». Την εποχή της εργασίας του Wigner, οι φυσικοί γνώριζαν ήδη ότι τα σωματίδια έχουν σπιν, ένα είδος εσωτερικής στροφορμής που καθορίζει πολλές πτυχές της συμπεριφοράς των σωματιδίων, συμπεριλαμβανομένου του εάν συμπεριφέρονται ως ύλη (όπως τα ηλεκτρόνια) ή ως φορείς αλληλεπιδράσεων (όπως τα φωτόνια). Ο Wigner έδειξε ότι, κατά βάθος, «το σπιν είναι απλώς μια ετικέτα που έχουν τα σωματίδια επειδή στον κόσμο υπάρχουν περιστροφές», δήλωσε η Nima Arkani-Hamed, φυσικός σωματιδίων στο Princeton.
Διαφορετικές αναπαραστάσεις της ομάδας Poincaré είναι σωματίδια με διαφορετικό αριθμό ετικετών σπιν ή βαθμούς ελευθερίας που επηρεάζονται από περιστροφές. Υπάρχουν, για παράδειγμα, σωματίδια με σπιν τριών βαθμών ελευθερίας. Αυτά τα σωματίδια περιστρέφονται με τον ίδιο τρόπο όπως τα οικεία μας τρισδιάστατα αντικείμενα. Όλα τα σωματίδια της ύλης, εν τω μεταξύ, έχουν σπιν με δύο βαθμούς ελευθερίας, που ονομάζονται «σπιν πάνω» και «σπιν κάτω», τα οποία περιστρέφονται διαφορετικά. Εάν περιστρέψετε ένα ηλεκτρόνιο κατά 360 μοίρες, η κατάστασή του θα αντιστραφεί, ακριβώς όπως ένα βέλος, όταν μετακινείται πάνω σε μια δισδιάστατη ταινία Möbius και επιστρέφει στην αρχική θέση δείχνοντας προς την αντίθετη φορά:
Στη φύση εμφανίζονται επίσης στοιχειώδη σωματίδια με μία και πέντε ετικέτες σπιν. Φαίνεται να λείπει μόνο μια αναπαράσταση της ομάδας Poincaré με τέσσερις ετικέτες σπιν.
”Η αντιστοιχία μεταξύ των στοιχειωδών σωματιδίων και των αναπαραστάσεων είναι τόσο ξεκάθαρη που ορισμένοι φυσικοί – όπως ο καθηγητής του Van Raamsdonk – τα εξισώνουν με αυτές. Άλλοι το βλέπουν ως ενοποίηση. «Η αναπαράσταση δεν είναι το σωματίδιο. Η αναπαράσταση είναι ένας τρόπος περιγραφής ορισμένων ιδιοτήτων του σωματιδίου», δήλωσε ο Sheldon Glashow, ένας βραβευμένος με Νόμπελ θεωρητικός στοιχειωδών σωματιδίων. «Ας μην συγχέουμε αυτά τα δύο.»
«Τα σωματίδια έχουν πολλές εσωτερικές καταστάσεις»
— Xiao-Gang Wen
Είτε υπάρχει διάκριση είτε όχι, η σχέση μεταξύ σωματιδιακής φυσικής και θεωρίας ομάδων έγινε τόσο πιο πλούσια όσο και πιο περίπλοκη κατά τη διάρκεια του 20ού αιώνα. Οι ανακαλύψεις έδειξαν ότι τα στοιχειώδη σωματίδια δεν έχουν μόνο το ελάχιστο σύνολο ετικετών που απαιτούνται για την πλοήγηση στο χωροχρόνο. Έχουν επιπλέον και κάποιες περιττές ετικέτες.
Σωματίδια με την ίδια ενέργεια, ορμή και σπιν συμπεριφέρονται πανομοιότυπα κάτω από τους 10 μετασχηματισμούς Poincaré, αλλά μπορεί να διαφέρουν με άλλους τρόπους. Για παράδειγμα, μπορούν να φέρουν διαφορετικές ποσότητες ηλεκτρικού φορτίου. Καθώς «ολόκληρος ο ζωολογικός κήπος σωματιδίων» (όπως το έθεσε ο Quinn) ανακαλύφθηκε στα μέσα του 20ου αιώνα, αποκαλύφθηκαν πρόσθετες διακρίσεις μεταξύ των σωματιδίων, απαιτώντας νέες ετικέτες που ονομάστηκαν «χρώμα» και «γεύση».
Ακριβώς όπως τα σωματίδια είναι αναπαραστάσεις της ομάδας Poincaré, οι θεωρητικοί συνειδητοποίησαν ότι οι επιπλέον ιδιότητές τους αντικατοπτρίζουν πρόσθετους τρόπους με τους οποίους αυτά μπορούν να μετασχηματιστούν. Αλλά αντί να μετακινούν αντικείμενα στο χωροχρόνο, αυτοί οι νέοι μετασχηματισμοί είναι πιο αφηρημένοι. Λέμε, λόγω έλλειψης καλύτερης λέξης, ότι αλλάζουν τις «εσωτερικές» καταστάσεις των σωματιδίων.
Πάρτε την ιδιότητα που είναι γνωστή ως χρώμα: Στη δεκαετία του 1960, οι φυσικοί διαπίστωσαν ότι τα κουάρκ, τα στοιχειώδη συστατικά των ατομικών πυρήνων, υπάρχουν σε έναν τυχαίο συνδυασμό τριών πιθανών καταστάσεων, τις οποίες ονόμαζαν «κόκκινο», «πράσινο» και «μπλε». Αυτές οι καταστάσεις δεν έχουν καμία σχέση με το πραγματικό χρώμα ή οποιαδήποτε άλλη ιδιότητα που μπορούμε να αντιληφθούμε. Είναι ο αριθμός των ετικετών που έχει σημασία: Τα κουάρκ, με τις τρεις ετικέτες τους, είναι αναπαραστάσεις μιας ομάδας μετασχηματισμών που ονομάζεται SU(3) που αποτελείται από το άπειρο πλήθος τρόπων μαθηματικής μίξης των τριών ετικετών.
Ενώ τα σωματίδια με χρώμα είναι αναπαραστάσεις της ομάδας συμμετρίας SU(3), τα σωματίδια με τις εσωτερικές ιδιότητες της γεύσης και του ηλεκτρικού φορτίου είναι αναπαραστάσεις των ομάδων συμμετρίας SU(2) και U(1), αντίστοιχα. Έτσι, το καθιερωμένο πρότυπο της φυσικής σωματιδίων – η κβαντική θεωρία πεδίου όλων των γνωστών στοιχειωδών σωματιδίων και οι αλληλεπιδράσεις τους – λέμε συχνά ότι αντιπροσωπεύει την ομάδα συμμετρίας SU(3)×SU(2)×U(1), που συνίσταται από όλους τους συνδυασμούς των πράξεων συμμετρίας στις τρεις υποομάδες. (Ότι τα σωματίδια μετασχηματίζονται επίσης και από την ομάδα Poincaré είναι προφανώς πολύ προφανές για να αναφερθεί.)
Το Καθιερωμένο Πρότυπο των στοιχειωδών σωματιδίων βασιλεύει μισό αιώνα μετά την εμφάνισή του. Ωστόσο, είναι μια ατελής περιγραφή του σύμπαντος. Κυρίως, του «διαφεύγει» η δύναμη της βαρύτητας, την οποία η κβαντική θεωρία πεδίου δεν μπορεί να χειριστεί πλήρως. Η γενική θεωρία της σχετικότητας του Albert Einstein περιγράφει ανεξάρτητα την βαρύτητα ως καμπύλωση του χωροχρόνου. Επιπλέον, η δομή των τριών τμημάτων του Καθιερωμένου Προτύπου SU(3)×SU(2)×U(1) εγείρει ερωτήματα. Δηλαδή: «Από πού στο διάολο προήλθαν όλα αυτά;» όπως το έθεσε ο Δημήτρης Νανόπουλος. «Εντάξει, ας υποθέσουμε ότι λειτουργεί», συνέχισε ο Νανόπουλος, ο οποίος είχε συνεισφέρει σημαντικά στις πρώτες μέρες του Καθιερωμένου Προτύπου. «Αλλά τι είναι αυτό το πράγμα; Δεν μπορεί να είναι τρεις ομάδες εκεί. Θέλω να πω, ο «Θεός» είναι καλύτερος από αυτό – ο Θεός σε εισαγωγικά.»
Τα σωματίδια «μπορεί να είναι ταλαντούμενες χορδές»
—Mary Gaillard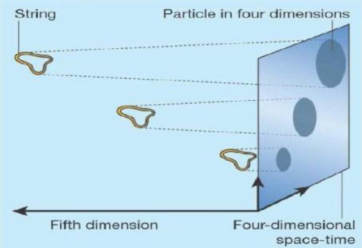
Στη δεκαετία του 1970, οι Glashow, Nανόπουλος και άλλοι προσπάθησαν να προσαρμόσουν τις ομάδες SU(3), SU(2) και U(1) μέσα σε μια μεγαλύτερη ομάδα μετασχηματισμών, με την υπόθεση ότι τα σωματίδια ήταν αναπαραστάσεις μιας ενιαίας ομάδας συμμετρίας στην αρχή του σύμπαντος. (Καθώς στη συνέχεια έσπασαν οι συμμετρίες, χάθηκε η ενοποιημένη απλότητα). Ο πιο φυσικός υποψήφιος για μια τέτοια «μεγάλη ενοποιημένη θεωρία» ήταν μια ομάδα συμμετρίας που ονομάζεται SU(5), αλλά τα πειράματα απέκλεισαν σύντομα αυτήν την επιλογή. Άλλες, λιγότερο ελκυστικές δυνατότητες παραμένουν στο παιχνίδι.
Οι ερευνητές επένδυσαν ακόμη μεγαλύτερες ελπίδες στη θεωρία χορδών: την ιδέα ότι αν μεγεθύνατε αρκετά σε σωματίδια, δεν θα βλέπετε σημεία αλλά μονοδιάστατες χορδές. Θα δείτε επίσης έξι επιπλέον χωρικές διαστάσεις, οι οποίες σύμφωνα με την θεωρία χορδών είναι κουλουριασμένες σε κάθε σημείο του οικείου μας τετραδιάστατου χωροχρόνου. Η γεωμετρία των μικρών διαστάσεων καθορίζει τις ιδιότητες των χορδών και επομένως τον μακροσκοπικό κόσμο. Οι «εσωτερικές» συμμετρίες σωματιδίων, όπως οι μετασχηματισμοί SU(3) που μετασχηματίζουν το χρώμα των κουάρκ, αποκτούν φυσική σημασία: Αυτοί οι μετασχηματισμοί αντιστοιχούν, στην εικόνα των χορδών, σε περιστροφές στις μικρές χωρικές διαστάσεις, ακριβώς όπως το σπιν εκφράζει περιστροφές στις μεγάλες διαστάσεις. «Η γεωμετρία σου δίνει συμμετρία η οποία σου δίνει σωματίδια, και όλα αυτά συμβαδίζουν», λέει ο Νανόπουλος.
Ωστόσο, εάν υπάρχουν χορδές ή επιπλέον διαστάσεις, είναι πολύ μικρές για να εντοπιστούν πειραματικά. Έτσι, εξαιτίας της βέβαιης απουσίας τους από τα πειράματα, αναπτύχθηκαν άλλες ιδέες. Στην τελευταία δεκαετία, δύο προσεγγίσεις έχουν προσελκύσει τα λαμπρότερα μυαλά στη σύγχρονη θεμελιώδη φυσική. Και οι δύο προσεγγίσεις ανανεώνουν ξανά την εικόνα των σωματιδίων.
Ένα σωματίδιο είναι μια «παραμόρφωση του ωκεανού κβαντοδυφίων (qubits)»
«Κάθε σωματίδιο είναι ένα κβαντικό κύμα. Το κύμα είναι μια παραμόρφωση του ωκεανού κβαντοδυφίων. »
—Xiao-Gang Wen
Η πρώτη από αυτές τις ερευνητικές προσπάθειες ξεκινάει από το σύνθημα «it-from-qubit (είναι από κβαντοδυφία)», το οποίο εκφράζει την υπόθεση ότι τα πάντα στο σύμπαν – όλα τα σωματίδια, καθώς και ο χωροχρονικός ιστός που αυτά τα σωματίδια είναι διασπαρμένα σαν βατόμουρα σε ένα σταφιδόψωμο – οφείλονται στα κβαντικά bit πληροφοριών, ή κβαντοδυφία (qubits).
Τι είναι το κβαντοδυφίο (qubit);
Έτσι ονομάζεται η βασική μονάδα μνήμης των κβαντικών υπολογιστών.
Στους γνωστούς κλασικούς υπολογιστές η βασική μονάδα πληροφορίας εγγραφής και επεξεργασίας της πληροφορίας στο δυαδικό σύστημα, με τα γνωστά ψηφία 0 και 1, χρησιμοποιείται ο όρος δυφίο (bit=binary digit). Το bit, στοιχειώδης μονάδα πληροφορίας, αποθηκεύεται σε κάποιο κλασικό φυσικό σύστημα που μπορεί να βρίσκεται σε δυο καταστάσεις όπως: οι δυο κατευθύνσεις μαγνήτισης, οι δυο θέσεις ενός διακόπτη, δυο τάσεις ηλεκτρικού ρεύματος κ.λπ.
Στους κβαντικούς υπολογιστές η βασική μονάδα εγγραφής δεν είναι ένα κλασικό σύστημα αλλά κβαντικό. Για παράδειγμα ένα άτομο υδρογόνου στη θεμελιώδη κατάσταση, όπου το μηδέν αντιπροσωπεύεται από την ηλεκτρονιακή κατάσταση με σπιν πάνω και το ένα από την κατάσταση με σπιν κάτω.
Συμβολίζουμε την κατάσταση με σπιν πάνω με |0> και την κατάσταση με σπιν κάτω με |1˃. Εφόσον το άτομο είναι ένα κβαντικό σύστημα, εκτός από τις δυο καταστάσεις |0> και |1>, θα είναι επίσης μια πραγματοποιήσιμη κατάσταση και κάθε γραμμικός συνδυασμός της μορφής |ψ> = α |0> + β |1>. όπου α2+ β2=1.
Και εδώ βρίσκεται η πηγή της θεμελιώδους διαφοράς μεταξύ ενός κλασικού και ενός κβαντικού υπολογιστή. Ότι στους κβαντικούς υπολογιστές η βασική μονάδα μνήμης μπορεί να βρίσκεται όχι μόνο στις καταστάσεις 0 και 1 αλλά και σε κάθε δυνατή επαλληλία (υπέρθεση) τους. Γι αυτό, στην περίπτωση των κβαντικών υπολογιστών μιλάμε για κβαντοδυφία (qubit=quantum bit).
Τα qubits μπορούν να αποθηκευτούν σε φυσικά συστήματα όπως τα bits μπορούν να αποθηκευτούν σε τρανζίστορ, αλλά μπορείτε να τα θεωρείτε πιο αφηρημένα, σαν την ίδια την πληροφορία.
Όταν υπάρχουν πολλά qubits, οι πιθανές καταστάσεις τους μπορούν να συμπλεχθούν, έτσι ώστε η κατάσταση του καθενός να εξαρτάται από τις καταστάσεις όλων των άλλων. Διαμέσου αυτών των ενδεχομένων ένας μικρός αριθμός συν-πλεγμένων qubits μπορεί να κωδικοποιήσει μια τεράστια ποσότητα πληροφοριών.
Στην έννοια it-from-qubit του σύμπαντος, εάν θέλετε να καταλάβετε τι είναι τα σωματίδια, πρέπει πρώτα να καταλάβετε τον χωροχρόνο. Το 2010, ο Van Raamsdonk, μέλος του στρατοπέδου it-from-qubit, έγραψε μια σημαντική εργασία, παρουσιάζοντας με τόλμη τι έδειχναν διάφοροι υπολογισμοί. Υποστήριξε ότι τα συν-πλεγμένα qubits μπορεί να ράβουν το ύφασμα χωροχρόνου.
Οι υπολογισμοί, τα νοητικά πειράματα και τα παραδείγματα απλών προσομοιώσεων των τελευταίων δεκαετιών δείχνουν ότι ο χωροχρόνος έχει «ολογραφικές» ιδιότητες: Είναι δυνατόν να κωδικοποιηθούν όλες οι πληροφορίες σχετικά με μια περιοχή χωροχρόνου σε βαθμούς ελευθερίας σε ένα χώρο με μία διάσταση λιγότερη – συχνά στην επιφάνεια της περιοχής. «Τα τελευταία 10 χρόνια, μάθαμε πολλά περισσότερα για το πώς λειτουργεί αυτή η κωδικοποίηση», υποστηρίζει ο Van Raamsdonk.
Το πιο εντυπωσιακό και συναρπαστικό για τους φυσικούς σχετικά με αυτήν την ολογραφική σχέση είναι ότι ο χωροχρόνος είναι καμπυλωμένος επειδή περιλαμβάνει τη βαρύτητα. Όμως, το σύστημα των λιγότερων διαστάσεων, που κωδικοποιεί τις πληροφορίες του καμπύλου χωροχρόνου, είναι ένα καθαρά κβαντικό σύστημα που δεν έχει καμία αίσθηση καμπυλότητας, βαρύτητας ή ακόμη και γεωμετρίας. Μπορεί να θεωρηθεί ως ένα σύστημα συν-μπλεγμένων qubits (κβαντοδυφίων).
Σύμφωνα με την υπόθεση it-from-qubit, οι ιδιότητες του χωροχρόνου προέρχονται ουσιαστικά από τον τρόπο με τον οποίο τα 0 και 1 εμπλέκονται μεταξύ τους. Η μακροχρόνια αναζήτηση για μια κβαντική περιγραφή της βαρύτητας γίνεται ζήτημα αναγνώρισης του μοτίβου σύμπλεξης των qubits που κωδικοποιούν το συγκεκριμένο είδος της χωροχρονικής δομής που συναντάμε στο πραγματικό σύμπαν.
Μέχρι στιγμής, οι ερευνητές γνωρίζουν πολύ περισσότερα για το πώς αυτό λειτουργεί σε απλοποιημένες προσομοιώσεις συμπάντων με αρνητικό καμπύλο χωροχρόνο, σαν σέλα – κυρίως επειδή είναι σχετικά εύκολη η μαθηματική επεξεργασία. Το σύμπαν μας, αντίθετα, έχει θετική καμπυλότητα. Αλλά, οι ερευνητές έχουν βρει, προς μεγάλη έκπληξή τους, ότι ανά πάσα στιγμή ο αρνητικός καμπύλος χωροχρόνος φαίνεται σαν ένα ολόγραμμα όπου εμφανίζονται σωματίδια. Δηλαδή, κάθε φορά που ένα σύστημα qubits κωδικοποιεί ολογραφικά μια περιοχή χωροχρόνου, υπάρχουν πάντα δομές συμπλεκομένων qubits που αντιστοιχούν σε τοπικά bits ενέργειας που επιπλέουν σε έναν υψηλότερων διαστάσεων κόσμο.
Κυρίως, οι αλγεβρικές πράξεις στα qubits, όταν μεταφράζονται σε όρους χωροχρόνου, «συμπεριφέρονται όπως οι περιστροφές που δρουν στα σωματίδια», δήλωσε ο Van Raamsdonk. «Συνειδητοποιείς ότι υπάρχει αυτή η εικόνα που κωδικοποιείται από αυτό το μη βαρυτικό κβαντικό σύστημα. Και κατά κάποιο τρόπο αυτός ο κώδικας, αν μπορείτε να τον αποκωδικοποιήσετε, σας λέει ότι υπάρχουν σωματίδια σε κάποιον άλλο χώρο.
Το γεγονός ότι ο ολογραφικός χωροχρόνος έχει πάντα αυτές τις καταστάσεις σωματιδίων είναι «στην πραγματικότητα ένα από τα πιο σημαντικά πράγματα που ξεχωρίζει αυτά τα ολογραφικά συστήματα από άλλα κβαντικά συστήματα». «Νομίζω ότι κανείς δεν καταλαβαίνει πραγματικά τον λόγο για τον οποίο τα ολογραφικά μοντέλα έχουν αυτήν την ιδιότητα.»
Είναι δελεαστικό να απεικονίζετε τα qubits με κάποιο είδος χωρικής διάταξης που δημιουργεί το ολογραφικό σύμπαν, ακριβώς όπως τα οικεία ολογράμματα που προέρχονται από χωρικές δομές. Αλλά στην πραγματικότητα, οι σχέσεις και οι αλληλεξαρτήσεις των qubits θα μπορούσαν να είναι πολύ πιο αφηρημένες, χωρίς καμία πραγματική φυσική ρύθμιση. «Δεν χρειάζεται να μιλάτε για αυτά τα 0 και 1 που ζουν σε έναν συγκεκριμένο χώρο», δήλωσε η Netta Engelhardt, φυσικός στο MIT, που κέρδισε πρόσφατα το βραβείο New Horizons στη Φυσική για τον υπολογισμό του κβαντικού περιεχομένου πληροφοριών των μαύρων οπών. «Μπορείτε να μιλήσετε για την αφηρημένη ύπαρξη των 0 και 1, και το πώς ένας τελεστής μπορεί να δράσει στα 0 και 1, και αυτές είναι πολύ πιο αφηρημένες μαθηματικές σχέσεις.»
Υπάρχουν σαφώς περισσότερα να καταλάβουμε. Αλλά αν η εικόνα «it-from-qubit (είναι από κβαντοδυφία)» είναι σωστή, τότε τα σωματίδια είναι ολογράμματα, όπως και ο χωροχρόνος. Ο πιο ακριβής ορισμός τους είναι σε όρους qubits (κβαντοδυσίων).
«Τα σωματίδια είναι αυτό που μετράμε στους ανιχνευτές»
—Nima Arkani-Hamed
Ένα άλλο στρατόπεδο ερευνητών που αυτοαποκαλούνται “amplitudeologists (πλατολόγοι;; )” επιδιώκει να στρέψει τους προβολείς στα ίδια τα σωματίδια.
Αυτοί οι ερευνητές υποστηρίζουν ότι η κβαντική θεωρία πεδίου, η τρέχουσα γλώσσα της σωματιδιακής φυσικής, «μας μιλάει πολύ περίπλοκα». Οι φυσικοί χρησιμοποιούν την κβαντική θεωρία πεδίου για να υπολογίσουν τους βασικούς τύπους που ονομάζονται πλάτη σκέδασης, που ανήκουν στα βασικότερα υπολογιστικά χαρακτηριστικά της πραγματικότητας. Όταν τα σωματίδια συγκρούονται, τα πλάτη δείχνουν πώς σκεδάζονται ή μορφοποιούνται τα σωματίδια. Οι αλληλεπιδράσεις των σωματιδίων φτιάχνουν τον κόσμο, οπότε ο τρόπος με τον οποίο οι φυσικοί ελέγχουν την περιγραφή τους για τον κόσμο, είναι να συγκρίνουν τους τύπους πλάτους σκέδασης με τα αποτελέσματα των συγκρούσεων των σωματιδίων σε επιταχυντές όπως ο Μεγάλος Επιταχυντής Αδρονίων.
Κανονικά, για να υπολογίσουν τα πλάτη, οι φυσικοί υπολογίζουν συστηματικά όλους τους πιθανούς τρόπους, με τους οποίους οι συγκρουόμενοι κυματισμοί ενδέχεται να αντηχούν διαμέσου των κβαντικών πεδίων που διαποτίζουν το σύμπαν, προτού παράξουν τα σταθερά σωματίδια που κινούνται μακριά από το σημείο σύγκρουσης. Περιέργως, οι υπολογισμοί που περιλαμβάνουν εκατοντάδες σελίδες άλγεβρας συχνά αποδίδουν, στο τέλος, έναν τύπο μιας γραμμής.
Οι amplitudeologists (πλατολόγοι) υποστηρίζουν ότι η εικόνα του πεδίου αποκρύβει απλούστερα μαθηματικά πρότυπα. Ο Arkani-Hamed, που ηγείται της της προσπάθειας, χαρακτήρισε τα κβαντικά πεδία «μια βολική φαντασία». «Στη φυσική πολύ συχνά μπαίνουμε σε ένα λάθος δίνοντας σάρκα και οστά σε έναν φορμαλισμό», είπε. «Αρχίζουμε τα ολισθήματα στη γλώσσα λέγοντας ότι τα κβαντικά πεδία είναι πραγματικά, και τα σωματίδια είναι διεγέρσεις. Μιλάμε για εικονικά σωματίδια κι όλα αυτά τα πράγματα – που όμως δεν κάνουν κλικ, κλικ, κλικ στον ανιχνευτή κανενός. »
Οι amplitudeologists (πλατολόγοι) πιστεύουν ότι υπάρχει μια μαθηματικά απλούστερη και πιο αληθινή εικόνα για τις αλληλεπιδράσεις των σωματιδίων. Σε ορισμένες περιπτώσεις, διαπιστώνουν ότι η προοπτική της θεωρίας ομάδων του Wigner για τα σωματίδια μπορεί να επεκταθεί ώστε να περιγράψει και τις αλληλεπιδράσεις τους, χωρίς καμία από τις συνηθισμένες ασυναρτησίες των κβαντικών πεδίων.
Ο Lance Dixon, ένας διακεκριμένος πλατολόγος στον επιταχυντή SLAC, εξήγησε ότι οι ερευνητές έχουν χρησιμοποιήσει τις περιστροφές Poincaré που μελετήθηκαν από τον Wigner για να υπολογίσουν άμεσα το «πλάτος τριών σημείων» – έναν τύπο που περιγράφει ένα σωματίδιο που διασπάται σε δύο σωματίδια. Έχουν δείξει επίσης ότι τα πλάτη τριών σημείων χρησιμεύουν ως δομικά στοιχεία των πλατών τεσσάρων και πλέον σημείων, που περιλαμβάνουν όλο και περισσότερα σωματίδια. Αυτές οι δυναμικές αλληλεπιδράσεις φαίνονται να οικοδομούνται εξ’ αρχής από τις βασικές συμμετρίες.
«Το πιο ωραίο», σύμφωνα με τον Dixon, είναι ότι τα πλάτη σκέδασης που εμπλέκουν τα βαρυτόνια, οι υποτιθέμενοι φορείς της βαρυτικής δύναμης, αποδεικνύεται ότι είναι το τετράγωνο πλάτους που περιλαμβάνει γλοιόνια, τα σωματίδια που συνδέουν μεταξύ τους τα κουάρκ. Η βαρύτητα συνδέεται με το ίδιο το ύφασμα του χωροχρόνου, ενώ τα γλοιόνια κινούνται στο χωροχρόνο. Ωστόσο, τα βαρυτόνια και τα γλοιόνια προέρχονται φαινομενικά από τις ίδιες συμμετρίες. «Αυτό είναι πολύ περίεργο και φυσικά δεν είναι ακόμα κατανοητό με ποσοτική λεπτομέρεια, επειδή οι εικόνες είναι τόσο διαφορετικές», λέει ο Dixon.
Ο Arkani-Hamed και οι συνεργάτες του, εν τω μεταξύ, έχουν βρει εντελώς νέες μαθηματικές «διατάξεις» που φτάνουν απευθείας στην απάντηση, όπως το amplituhedron (πλατύεδρο) – ένα γεωμετρικό αντικείμενο που κωδικοποιεί πλάτη σκέδασης σωματιδίων στον όγκο του. Διώχνει την εικόνα των σωματιδίων που συγκρούονται στο χωροχρόνο και προκαλούν αλυσιδωτές αντιδράσεις αιτίας και αποτελέσματος. «Προσπαθούμε να βρούμε αυτά τα αντικείμενα εκεί έξω στον πλατωνικό κόσμο των ιδεών, που μας δίνουν τις [αιτιώδεις] ιδιότητες αυτόματα», δήλωσε ο Arkani-Hamed. «Τότε θα μπορούμε να πούμε, Αχα, τώρα μπορώ να δω γιατί αυτή η εικόνα μπορεί να ερμηνευθεί ως εξέλιξη.»
Νίμα Αρκάνι-Χαμέντ
Το «It-from-qubit (Είναι από κβαντοδυφία)» και η amplitudeology (πλατολογία) προσεγγίζουν τα μεγάλα ερωτήματα τόσο διαφορετικά που είναι δύσκολο να πούμε αν αυτές οι δύο εικόνες αλληλοσυμπληρώνονται ή έρχονται σε αντίθεση μεταξύ τους.
Σύμφωνα με την Netta Engelhardt, μια πιο σύνθετη διατύπωση της ερώτησης του τίτλου, «Τι είναι ένα σωματίδιο;» τίθεται ως «Ποια είναι τα θεμελιώδη δομικά στοιχεία του σύμπαντος στις πιο θεμελιώδεις του κλίμακες;»
Και μέχρι να βρεθεί μια πλήρης κβαντική θεωρία της βαρύτητας και του χωροχρόνου, η σύντομη απάντηση είναι: «Δεν γνωρίζουμε».
διαβάστε περισσότερες λεπτομέρειες στο άρθρο της Natalie Wolchover, «What Is a Particle?» στο Quantamagazine
Σωματίδιο είναι μια ‘Κβαντική Διέγερση ενός Πεδίου’
«Τι είναι ένα σωματίδιο για έναν φυσικό; Είναι μια κβαντική διέγερση ενός πεδίου. Γράφουμε την φυσική σωματιδίων σε μια μαθηματική γλώσσα που ονομάζεται κβαντική θεωρία πεδίου. Δεδομένου ότι υπάρχουν πολλά διαφορετικά πεδία, με κάθε πεδίο να έχει διαφορετικές ιδιότητες και διαφορετικές διεγέρσεις ανάλογα με τις ιδιότητες, αυτές τις διεγέρσεις μπορούμε να τις θεωρήσουμε ως σωματίδια.»
—Helen Quinn
Στη δεκαετία του 1930 η εικόνα έγινε ακόμη πιο παράξενη. Οι φυσικοί συνειδητοποίησαν ότι οι κυματοσυναρτήσεις πολλών μεμονωμένων φωτονίων συμπεριφέρονται συλλογικά σαν ένα μόνο κύμα που διαδίδεται μέσω σύμφωνων ηλεκτρικών και μαγνητικών πεδίων – ακριβώς όπως η κλασική εικόνα του φωτός που ανακαλύφθηκε τον 19ο αιώνα από τον James Clerk Maxwell. Αυτοί οι ερευνητές διαπίστωσαν ότι θα μπορούσαν να «κβαντώσουν» την κλασική θεωρία πεδίων, περιορίζοντας τα πεδία, ώστε να μπορούν να ταλαντώνονται μόνο σε διακριτές ποσότητες γνωστές ως «κβάντα» των πεδίων. Εκτός από τα φωτόνια – τα κβάντα του φωτός – ο Paul Dirac και άλλοι ανακάλυψαν ότι η ιδέα θα μπορούσε να επεκταθεί σε ηλεκτρόνια και σε οτιδήποτε άλλο: Σύμφωνα με την κβαντική θεωρία πεδίου, τα σωματίδια είναι διεγέρσεις των κβαντικών πεδίων που γεμίζουν όλο το χώρο.
Θεωρώντας την ύπαρξη αυτών των πιο θεμελιωδών πεδίων, η κβαντική θεωρία πεδίου απογύμνωσε την κατάσταση των σωματιδίων, χαρακτηρίζοντάς τα ως απλά μπιτ ενέργειας που θέτουν τα πεδία σε «παφλασμό». Ωστόσο, παρά το οντολογικό φορτίο των πανταχού παρόντων πεδίων, η κβαντική θεωρία πεδίου έγινε η κοινή γλώσσα της σωματιδιακής φυσικής, επειδή επιτρέπει στους ερευνητές να υπολογίζουν με ακρίβεια τι συμβαίνει όταν αλληλεπιδρούν σωματίδια – οι αλληλεπιδράσεις σωματιδίων είναι, σε βασικό επίπεδο, ο τρόπος με τον οποίο ο κόσμος συναρμολογείται.
Καθώς οι φυσικοί ανακάλυπταν όλο και περισσότερα σωματίδια και τα σχετικά πεδία τους, αναπτύχθηκε μια παράλληλη προοπτική. Οι ιδιότητες αυτών των σωματιδίων και πεδίων φαίνονταν να ακολουθούν αριθμητικά μοτίβα. Επεκτείνοντας αυτά τα μοτίβα, οι φυσικοί μπόρεσαν να προβλέψουν την ύπαρξη περισσότερων σωματιδίων. «Άπαξ και κωδικοποιήσετε τα μοτίβα που παρατηρείτε στα μαθηματικά, τα μαθηματικά διαθέτουν προβλεπτικότητα. Σου λένε περισσότερα πράγματα από αυτά που μπορείς να παρατηρήσεις, επισημαίνει η Helen Quinn, φυσικός σωματιδίων στο Πανεπιστήμιο του Στάνφορντ.
Τα μοτίβα υποδεικνύουν επίσης μια πιο αφηρημένη και ενδεχομένως βαθύτερη οπτική για το τι είναι στ’ αλήθεια τα σωματίδια.
Ένα σωματίδιο είναι μια «μη-αναγώγιμη αναπαράσταση ομάδας»
«Τα σωματίδια περιγράφονται στο ελάχιστο από μη αναγώγιμες αναπαραστάσεις της ομάδας Poincaré.»
— Sheldon Glashow
Ο Mark Van Raamsdonk θυμάται το ξεκίνημα του πρώτου μαθήματος της κβαντικής θεωρίας πεδίου, ως μεταπτυχιακός φοιτητής στο Πανεπιστήμιο του Πρίνστον. Ο καθηγητής μπήκε στην αίθουσα, κοίταξε τους μαθητές και ρώτησε: «Τι είναι ένα σωματίδιο;»
«Μια μη αναγωγίσιμη αναπαράσταση της ομάδας Poincaré», απάντησε ένας διαβασμένος συμφοιτητής.
Λαμβάνοντας τον προφανώς σωστό ορισμό ως γενική γνώση, ο καθηγητής παρέλειψε οποιαδήποτε εξήγηση και άρχισε μια ακατανόητη σειρά διαλέξεων. «Όλο αυτό το εξάμηνο δεν έμαθα τίποτα από το μάθημα», δήλωσε ο Van Raamsdonk, ο οποίος είναι πλέον ένας αναγνωρισμένος θεωρητικός φυσικός στο Πανεπιστήμιο του Βανκούβερ.
Είναι μια βαθύτερη συνηθισμένη απάντηση των ανθρώπων που γνωρίζουν: Τα σωματίδια είναι «αναπαραστάσεις» των «ομάδων συμμετρίας», οι οποίες είναι σύνολα μετασχηματισμών που μπορούν να εφαρμοστούν σε αντικείμενα.
Πάρτε, για παράδειγμα, ένα ισόπλευρο τρίγωνο. Περιστρέφοντάς το κατά 120 ή 240 μοίρες, ή ανακλώντας ως προς την ευθεία που διέρχεται από κάποιο ύψος του, ή μη κάνοντας τίποτα, όλα αφήνουν το τρίγωνο αναλλοίωτο να φαίνεται όπως ήταν πριν. Αυτές οι έξι συμμετρίες σχηματίζουν μια ομάδα. Η ομάδα μπορεί να εκφραστεί ως ένα σύνολο μαθηματικών πινάκων – διατάξεις αριθμών που, όταν πολλαπλασιαστούν με τις συντεταγμένες ισόπλευρου τριγώνου, δίνουν τις ίδιες συντεταγμένες. Ένα τέτοιο σύνολο πινάκων είναι μια «αναπαράσταση» της ομάδας συμμετρίας.
Με παρόμοιο τρόπο, τα ηλεκτρόνια, τα φωτόνια και άλλα στοιχειώδη σωματίδια είναι αντικείμενα που ουσιαστικά παραμένουν τα ίδια όταν δρα σ’ αυτά μια συγκεκριμένη ομάδα. Δηλαδή, τα σωματίδια είναι αναπαραστάσεις της ομάδας Poincaré: η ομάδα των 10 (μετασχηματισμών) τρόπων μετακίνησης στο χωροχρονικό συνεχές. Τα αντικείμενα μπορούν να μετακινηθούν σε τρεις χωρικές κατευθύνσεις ή να μετατοπιστούν χρονικά. Μπορούν επίσης να περιστραφούν σε τρεις κατευθύνσεις ή να αποκτήσουν ορμή σε οποιαδήποτε από αυτές τις κατευθύνσεις. Το 1939, ο φυσικο-μαθηματικός Eugene Wigner όρισε τα σωματίδια ως τα απλούστερα δυνατά αντικείμενα που μπορούν να μετατοπιστούν, να περιστραφούν και να ωθηθούν.Για να μετασχηματιστεί σωστά ένα αντικείμενο κάτω από αυτούς τους 10 μετασχηματισμούς Poincaré, συνειδητοποίησε ότι πρέπει να έχει ένα ορισμένο ελάχιστο σύνολο ιδιοτήτων και τα σωματίδια να έχουν αυτές τις ιδιότητες. H μια είναι η ενέργεια. Κατά βάθος, η ενέργεια είναι απλά η ιδιότητα που παραμένει ίδια όταν το αντικείμενο μετατοπίζεται χρονικά. Η ορμή είναι η ιδιότητα που παραμένει ίδια όταν το αντικείμενο μετατοπίζεται στον χώρο.
Μια τρίτη ιδιότητα απαιτείται για τον προσδιορισμό του τρόπου με τον οποίο τα σωματίδια αλλάζουν κάτω από τον συνδυασμό μετασχηματισμών χωρικών περιστροφών και μετατοπίσεων (που, μαζί, είναι περιστροφές στο χωροχρόνο). Αυτή η ιδιότητα-κλειδί είναι το «σπιν». Την εποχή της εργασίας του Wigner, οι φυσικοί γνώριζαν ήδη ότι τα σωματίδια έχουν σπιν, ένα είδος εσωτερικής στροφορμής που καθορίζει πολλές πτυχές της συμπεριφοράς των σωματιδίων, συμπεριλαμβανομένου του εάν συμπεριφέρονται ως ύλη (όπως τα ηλεκτρόνια) ή ως φορείς αλληλεπιδράσεων (όπως τα φωτόνια). Ο Wigner έδειξε ότι, κατά βάθος, «το σπιν είναι απλώς μια ετικέτα που έχουν τα σωματίδια επειδή στον κόσμο υπάρχουν περιστροφές», δήλωσε η Nima Arkani-Hamed, φυσικός σωματιδίων στο Princeton.
Διαφορετικές αναπαραστάσεις της ομάδας Poincaré είναι σωματίδια με διαφορετικό αριθμό ετικετών σπιν ή βαθμούς ελευθερίας που επηρεάζονται από περιστροφές. Υπάρχουν, για παράδειγμα, σωματίδια με σπιν τριών βαθμών ελευθερίας. Αυτά τα σωματίδια περιστρέφονται με τον ίδιο τρόπο όπως τα οικεία μας τρισδιάστατα αντικείμενα. Όλα τα σωματίδια της ύλης, εν τω μεταξύ, έχουν σπιν με δύο βαθμούς ελευθερίας, που ονομάζονται «σπιν πάνω» και «σπιν κάτω», τα οποία περιστρέφονται διαφορετικά. Εάν περιστρέψετε ένα ηλεκτρόνιο κατά 360 μοίρες, η κατάστασή του θα αντιστραφεί, ακριβώς όπως ένα βέλος, όταν μετακινείται πάνω σε μια δισδιάστατη ταινία Möbius και επιστρέφει στην αρχική θέση δείχνοντας προς την αντίθετη φορά:
Στη φύση εμφανίζονται επίσης στοιχειώδη σωματίδια με μία και πέντε ετικέτες σπιν. Φαίνεται να λείπει μόνο μια αναπαράσταση της ομάδας Poincaré με τέσσερις ετικέτες σπιν.
”Η αντιστοιχία μεταξύ των στοιχειωδών σωματιδίων και των αναπαραστάσεων είναι τόσο ξεκάθαρη που ορισμένοι φυσικοί – όπως ο καθηγητής του Van Raamsdonk – τα εξισώνουν με αυτές. Άλλοι το βλέπουν ως ενοποίηση. «Η αναπαράσταση δεν είναι το σωματίδιο. Η αναπαράσταση είναι ένας τρόπος περιγραφής ορισμένων ιδιοτήτων του σωματιδίου», δήλωσε ο Sheldon Glashow, ένας βραβευμένος με Νόμπελ θεωρητικός στοιχειωδών σωματιδίων. «Ας μην συγχέουμε αυτά τα δύο.»
«Τα σωματίδια έχουν πολλές εσωτερικές καταστάσεις»
— Xiao-Gang Wen
Είτε υπάρχει διάκριση είτε όχι, η σχέση μεταξύ σωματιδιακής φυσικής και θεωρίας ομάδων έγινε τόσο πιο πλούσια όσο και πιο περίπλοκη κατά τη διάρκεια του 20ού αιώνα. Οι ανακαλύψεις έδειξαν ότι τα στοιχειώδη σωματίδια δεν έχουν μόνο το ελάχιστο σύνολο ετικετών που απαιτούνται για την πλοήγηση στο χωροχρόνο. Έχουν επιπλέον και κάποιες περιττές ετικέτες.
Σωματίδια με την ίδια ενέργεια, ορμή και σπιν συμπεριφέρονται πανομοιότυπα κάτω από τους 10 μετασχηματισμούς Poincaré, αλλά μπορεί να διαφέρουν με άλλους τρόπους. Για παράδειγμα, μπορούν να φέρουν διαφορετικές ποσότητες ηλεκτρικού φορτίου. Καθώς «ολόκληρος ο ζωολογικός κήπος σωματιδίων» (όπως το έθεσε ο Quinn) ανακαλύφθηκε στα μέσα του 20ου αιώνα, αποκαλύφθηκαν πρόσθετες διακρίσεις μεταξύ των σωματιδίων, απαιτώντας νέες ετικέτες που ονομάστηκαν «χρώμα» και «γεύση».
Ακριβώς όπως τα σωματίδια είναι αναπαραστάσεις της ομάδας Poincaré, οι θεωρητικοί συνειδητοποίησαν ότι οι επιπλέον ιδιότητές τους αντικατοπτρίζουν πρόσθετους τρόπους με τους οποίους αυτά μπορούν να μετασχηματιστούν. Αλλά αντί να μετακινούν αντικείμενα στο χωροχρόνο, αυτοί οι νέοι μετασχηματισμοί είναι πιο αφηρημένοι. Λέμε, λόγω έλλειψης καλύτερης λέξης, ότι αλλάζουν τις «εσωτερικές» καταστάσεις των σωματιδίων.
Πάρτε την ιδιότητα που είναι γνωστή ως χρώμα: Στη δεκαετία του 1960, οι φυσικοί διαπίστωσαν ότι τα κουάρκ, τα στοιχειώδη συστατικά των ατομικών πυρήνων, υπάρχουν σε έναν τυχαίο συνδυασμό τριών πιθανών καταστάσεων, τις οποίες ονόμαζαν «κόκκινο», «πράσινο» και «μπλε». Αυτές οι καταστάσεις δεν έχουν καμία σχέση με το πραγματικό χρώμα ή οποιαδήποτε άλλη ιδιότητα που μπορούμε να αντιληφθούμε. Είναι ο αριθμός των ετικετών που έχει σημασία: Τα κουάρκ, με τις τρεις ετικέτες τους, είναι αναπαραστάσεις μιας ομάδας μετασχηματισμών που ονομάζεται SU(3) που αποτελείται από το άπειρο πλήθος τρόπων μαθηματικής μίξης των τριών ετικετών.
Ενώ τα σωματίδια με χρώμα είναι αναπαραστάσεις της ομάδας συμμετρίας SU(3), τα σωματίδια με τις εσωτερικές ιδιότητες της γεύσης και του ηλεκτρικού φορτίου είναι αναπαραστάσεις των ομάδων συμμετρίας SU(2) και U(1), αντίστοιχα. Έτσι, το καθιερωμένο πρότυπο της φυσικής σωματιδίων – η κβαντική θεωρία πεδίου όλων των γνωστών στοιχειωδών σωματιδίων και οι αλληλεπιδράσεις τους – λέμε συχνά ότι αντιπροσωπεύει την ομάδα συμμετρίας SU(3)×SU(2)×U(1), που συνίσταται από όλους τους συνδυασμούς των πράξεων συμμετρίας στις τρεις υποομάδες. (Ότι τα σωματίδια μετασχηματίζονται επίσης και από την ομάδα Poincaré είναι προφανώς πολύ προφανές για να αναφερθεί.)
Το Καθιερωμένο Πρότυπο των στοιχειωδών σωματιδίων βασιλεύει μισό αιώνα μετά την εμφάνισή του. Ωστόσο, είναι μια ατελής περιγραφή του σύμπαντος. Κυρίως, του «διαφεύγει» η δύναμη της βαρύτητας, την οποία η κβαντική θεωρία πεδίου δεν μπορεί να χειριστεί πλήρως. Η γενική θεωρία της σχετικότητας του Albert Einstein περιγράφει ανεξάρτητα την βαρύτητα ως καμπύλωση του χωροχρόνου. Επιπλέον, η δομή των τριών τμημάτων του Καθιερωμένου Προτύπου SU(3)×SU(2)×U(1) εγείρει ερωτήματα. Δηλαδή: «Από πού στο διάολο προήλθαν όλα αυτά;» όπως το έθεσε ο Δημήτρης Νανόπουλος. «Εντάξει, ας υποθέσουμε ότι λειτουργεί», συνέχισε ο Νανόπουλος, ο οποίος είχε συνεισφέρει σημαντικά στις πρώτες μέρες του Καθιερωμένου Προτύπου. «Αλλά τι είναι αυτό το πράγμα; Δεν μπορεί να είναι τρεις ομάδες εκεί. Θέλω να πω, ο «Θεός» είναι καλύτερος από αυτό – ο Θεός σε εισαγωγικά.»
Τα σωματίδια «μπορεί να είναι ταλαντούμενες χορδές»
—Mary Gaillard
Στη δεκαετία του 1970, οι Glashow, Nανόπουλος και άλλοι προσπάθησαν να προσαρμόσουν τις ομάδες SU(3), SU(2) και U(1) μέσα σε μια μεγαλύτερη ομάδα μετασχηματισμών, με την υπόθεση ότι τα σωματίδια ήταν αναπαραστάσεις μιας ενιαίας ομάδας συμμετρίας στην αρχή του σύμπαντος. (Καθώς στη συνέχεια έσπασαν οι συμμετρίες, χάθηκε η ενοποιημένη απλότητα). Ο πιο φυσικός υποψήφιος για μια τέτοια «μεγάλη ενοποιημένη θεωρία» ήταν μια ομάδα συμμετρίας που ονομάζεται SU(5), αλλά τα πειράματα απέκλεισαν σύντομα αυτήν την επιλογή. Άλλες, λιγότερο ελκυστικές δυνατότητες παραμένουν στο παιχνίδι.
Οι ερευνητές επένδυσαν ακόμη μεγαλύτερες ελπίδες στη θεωρία χορδών: την ιδέα ότι αν μεγεθύνατε αρκετά σε σωματίδια, δεν θα βλέπετε σημεία αλλά μονοδιάστατες χορδές. Θα δείτε επίσης έξι επιπλέον χωρικές διαστάσεις, οι οποίες σύμφωνα με την θεωρία χορδών είναι κουλουριασμένες σε κάθε σημείο του οικείου μας τετραδιάστατου χωροχρόνου. Η γεωμετρία των μικρών διαστάσεων καθορίζει τις ιδιότητες των χορδών και επομένως τον μακροσκοπικό κόσμο. Οι «εσωτερικές» συμμετρίες σωματιδίων, όπως οι μετασχηματισμοί SU(3) που μετασχηματίζουν το χρώμα των κουάρκ, αποκτούν φυσική σημασία: Αυτοί οι μετασχηματισμοί αντιστοιχούν, στην εικόνα των χορδών, σε περιστροφές στις μικρές χωρικές διαστάσεις, ακριβώς όπως το σπιν εκφράζει περιστροφές στις μεγάλες διαστάσεις. «Η γεωμετρία σου δίνει συμμετρία η οποία σου δίνει σωματίδια, και όλα αυτά συμβαδίζουν», λέει ο Νανόπουλος.
Ωστόσο, εάν υπάρχουν χορδές ή επιπλέον διαστάσεις, είναι πολύ μικρές για να εντοπιστούν πειραματικά. Έτσι, εξαιτίας της βέβαιης απουσίας τους από τα πειράματα, αναπτύχθηκαν άλλες ιδέες. Στην τελευταία δεκαετία, δύο προσεγγίσεις έχουν προσελκύσει τα λαμπρότερα μυαλά στη σύγχρονη θεμελιώδη φυσική. Και οι δύο προσεγγίσεις ανανεώνουν ξανά την εικόνα των σωματιδίων.
Ένα σωματίδιο είναι μια «παραμόρφωση του ωκεανού κβαντοδυφίων (qubits)»
«Κάθε σωματίδιο είναι ένα κβαντικό κύμα. Το κύμα είναι μια παραμόρφωση του ωκεανού κβαντοδυφίων. »
—Xiao-Gang Wen
Η πρώτη από αυτές τις ερευνητικές προσπάθειες ξεκινάει από το σύνθημα «it-from-qubit (είναι από κβαντοδυφία)», το οποίο εκφράζει την υπόθεση ότι τα πάντα στο σύμπαν – όλα τα σωματίδια, καθώς και ο χωροχρονικός ιστός που αυτά τα σωματίδια είναι διασπαρμένα σαν βατόμουρα σε ένα σταφιδόψωμο – οφείλονται στα κβαντικά bit πληροφοριών, ή κβαντοδυφία (qubits).
Τι είναι το κβαντοδυφίο (qubit);
Έτσι ονομάζεται η βασική μονάδα μνήμης των κβαντικών υπολογιστών.
Στους γνωστούς κλασικούς υπολογιστές η βασική μονάδα πληροφορίας εγγραφής και επεξεργασίας της πληροφορίας στο δυαδικό σύστημα, με τα γνωστά ψηφία 0 και 1, χρησιμοποιείται ο όρος δυφίο (bit=binary digit). Το bit, στοιχειώδης μονάδα πληροφορίας, αποθηκεύεται σε κάποιο κλασικό φυσικό σύστημα που μπορεί να βρίσκεται σε δυο καταστάσεις όπως: οι δυο κατευθύνσεις μαγνήτισης, οι δυο θέσεις ενός διακόπτη, δυο τάσεις ηλεκτρικού ρεύματος κ.λπ.
Στους κβαντικούς υπολογιστές η βασική μονάδα εγγραφής δεν είναι ένα κλασικό σύστημα αλλά κβαντικό. Για παράδειγμα ένα άτομο υδρογόνου στη θεμελιώδη κατάσταση, όπου το μηδέν αντιπροσωπεύεται από την ηλεκτρονιακή κατάσταση με σπιν πάνω και το ένα από την κατάσταση με σπιν κάτω.
Συμβολίζουμε την κατάσταση με σπιν πάνω με |0> και την κατάσταση με σπιν κάτω με |1˃. Εφόσον το άτομο είναι ένα κβαντικό σύστημα, εκτός από τις δυο καταστάσεις |0> και |1>, θα είναι επίσης μια πραγματοποιήσιμη κατάσταση και κάθε γραμμικός συνδυασμός της μορφής |ψ> = α |0> + β |1>. όπου α2+ β2=1.
Και εδώ βρίσκεται η πηγή της θεμελιώδους διαφοράς μεταξύ ενός κλασικού και ενός κβαντικού υπολογιστή. Ότι στους κβαντικούς υπολογιστές η βασική μονάδα μνήμης μπορεί να βρίσκεται όχι μόνο στις καταστάσεις 0 και 1 αλλά και σε κάθε δυνατή επαλληλία (υπέρθεση) τους. Γι αυτό, στην περίπτωση των κβαντικών υπολογιστών μιλάμε για κβαντοδυφία (qubit=quantum bit).
Τα qubits μπορούν να αποθηκευτούν σε φυσικά συστήματα όπως τα bits μπορούν να αποθηκευτούν σε τρανζίστορ, αλλά μπορείτε να τα θεωρείτε πιο αφηρημένα, σαν την ίδια την πληροφορία.
Όταν υπάρχουν πολλά qubits, οι πιθανές καταστάσεις τους μπορούν να συμπλεχθούν, έτσι ώστε η κατάσταση του καθενός να εξαρτάται από τις καταστάσεις όλων των άλλων. Διαμέσου αυτών των ενδεχομένων ένας μικρός αριθμός συν-πλεγμένων qubits μπορεί να κωδικοποιήσει μια τεράστια ποσότητα πληροφοριών.
Στην έννοια it-from-qubit του σύμπαντος, εάν θέλετε να καταλάβετε τι είναι τα σωματίδια, πρέπει πρώτα να καταλάβετε τον χωροχρόνο. Το 2010, ο Van Raamsdonk, μέλος του στρατοπέδου it-from-qubit, έγραψε μια σημαντική εργασία, παρουσιάζοντας με τόλμη τι έδειχναν διάφοροι υπολογισμοί. Υποστήριξε ότι τα συν-πλεγμένα qubits μπορεί να ράβουν το ύφασμα χωροχρόνου.
Οι υπολογισμοί, τα νοητικά πειράματα και τα παραδείγματα απλών προσομοιώσεων των τελευταίων δεκαετιών δείχνουν ότι ο χωροχρόνος έχει «ολογραφικές» ιδιότητες: Είναι δυνατόν να κωδικοποιηθούν όλες οι πληροφορίες σχετικά με μια περιοχή χωροχρόνου σε βαθμούς ελευθερίας σε ένα χώρο με μία διάσταση λιγότερη – συχνά στην επιφάνεια της περιοχής. «Τα τελευταία 10 χρόνια, μάθαμε πολλά περισσότερα για το πώς λειτουργεί αυτή η κωδικοποίηση», υποστηρίζει ο Van Raamsdonk.
Το πιο εντυπωσιακό και συναρπαστικό για τους φυσικούς σχετικά με αυτήν την ολογραφική σχέση είναι ότι ο χωροχρόνος είναι καμπυλωμένος επειδή περιλαμβάνει τη βαρύτητα. Όμως, το σύστημα των λιγότερων διαστάσεων, που κωδικοποιεί τις πληροφορίες του καμπύλου χωροχρόνου, είναι ένα καθαρά κβαντικό σύστημα που δεν έχει καμία αίσθηση καμπυλότητας, βαρύτητας ή ακόμη και γεωμετρίας. Μπορεί να θεωρηθεί ως ένα σύστημα συν-μπλεγμένων qubits (κβαντοδυφίων).
Σύμφωνα με την υπόθεση it-from-qubit, οι ιδιότητες του χωροχρόνου προέρχονται ουσιαστικά από τον τρόπο με τον οποίο τα 0 και 1 εμπλέκονται μεταξύ τους. Η μακροχρόνια αναζήτηση για μια κβαντική περιγραφή της βαρύτητας γίνεται ζήτημα αναγνώρισης του μοτίβου σύμπλεξης των qubits που κωδικοποιούν το συγκεκριμένο είδος της χωροχρονικής δομής που συναντάμε στο πραγματικό σύμπαν.
Μέχρι στιγμής, οι ερευνητές γνωρίζουν πολύ περισσότερα για το πώς αυτό λειτουργεί σε απλοποιημένες προσομοιώσεις συμπάντων με αρνητικό καμπύλο χωροχρόνο, σαν σέλα – κυρίως επειδή είναι σχετικά εύκολη η μαθηματική επεξεργασία. Το σύμπαν μας, αντίθετα, έχει θετική καμπυλότητα. Αλλά, οι ερευνητές έχουν βρει, προς μεγάλη έκπληξή τους, ότι ανά πάσα στιγμή ο αρνητικός καμπύλος χωροχρόνος φαίνεται σαν ένα ολόγραμμα όπου εμφανίζονται σωματίδια. Δηλαδή, κάθε φορά που ένα σύστημα qubits κωδικοποιεί ολογραφικά μια περιοχή χωροχρόνου, υπάρχουν πάντα δομές συμπλεκομένων qubits που αντιστοιχούν σε τοπικά bits ενέργειας που επιπλέουν σε έναν υψηλότερων διαστάσεων κόσμο.
Κυρίως, οι αλγεβρικές πράξεις στα qubits, όταν μεταφράζονται σε όρους χωροχρόνου, «συμπεριφέρονται όπως οι περιστροφές που δρουν στα σωματίδια», δήλωσε ο Van Raamsdonk. «Συνειδητοποιείς ότι υπάρχει αυτή η εικόνα που κωδικοποιείται από αυτό το μη βαρυτικό κβαντικό σύστημα. Και κατά κάποιο τρόπο αυτός ο κώδικας, αν μπορείτε να τον αποκωδικοποιήσετε, σας λέει ότι υπάρχουν σωματίδια σε κάποιον άλλο χώρο.
Το γεγονός ότι ο ολογραφικός χωροχρόνος έχει πάντα αυτές τις καταστάσεις σωματιδίων είναι «στην πραγματικότητα ένα από τα πιο σημαντικά πράγματα που ξεχωρίζει αυτά τα ολογραφικά συστήματα από άλλα κβαντικά συστήματα». «Νομίζω ότι κανείς δεν καταλαβαίνει πραγματικά τον λόγο για τον οποίο τα ολογραφικά μοντέλα έχουν αυτήν την ιδιότητα.»
Είναι δελεαστικό να απεικονίζετε τα qubits με κάποιο είδος χωρικής διάταξης που δημιουργεί το ολογραφικό σύμπαν, ακριβώς όπως τα οικεία ολογράμματα που προέρχονται από χωρικές δομές. Αλλά στην πραγματικότητα, οι σχέσεις και οι αλληλεξαρτήσεις των qubits θα μπορούσαν να είναι πολύ πιο αφηρημένες, χωρίς καμία πραγματική φυσική ρύθμιση. «Δεν χρειάζεται να μιλάτε για αυτά τα 0 και 1 που ζουν σε έναν συγκεκριμένο χώρο», δήλωσε η Netta Engelhardt, φυσικός στο MIT, που κέρδισε πρόσφατα το βραβείο New Horizons στη Φυσική για τον υπολογισμό του κβαντικού περιεχομένου πληροφοριών των μαύρων οπών. «Μπορείτε να μιλήσετε για την αφηρημένη ύπαρξη των 0 και 1, και το πώς ένας τελεστής μπορεί να δράσει στα 0 και 1, και αυτές είναι πολύ πιο αφηρημένες μαθηματικές σχέσεις.»
Υπάρχουν σαφώς περισσότερα να καταλάβουμε. Αλλά αν η εικόνα «it-from-qubit (είναι από κβαντοδυφία)» είναι σωστή, τότε τα σωματίδια είναι ολογράμματα, όπως και ο χωροχρόνος. Ο πιο ακριβής ορισμός τους είναι σε όρους qubits (κβαντοδυσίων).
«Τα σωματίδια είναι αυτό που μετράμε στους ανιχνευτές»
—Nima Arkani-Hamed
Ένα άλλο στρατόπεδο ερευνητών που αυτοαποκαλούνται “amplitudeologists (πλατολόγοι;; )” επιδιώκει να στρέψει τους προβολείς στα ίδια τα σωματίδια.Αυτοί οι ερευνητές υποστηρίζουν ότι η κβαντική θεωρία πεδίου, η τρέχουσα γλώσσα της σωματιδιακής φυσικής, «μας μιλάει πολύ περίπλοκα». Οι φυσικοί χρησιμοποιούν την κβαντική θεωρία πεδίου για να υπολογίσουν τους βασικούς τύπους που ονομάζονται πλάτη σκέδασης, που ανήκουν στα βασικότερα υπολογιστικά χαρακτηριστικά της πραγματικότητας. Όταν τα σωματίδια συγκρούονται, τα πλάτη δείχνουν πώς σκεδάζονται ή μορφοποιούνται τα σωματίδια. Οι αλληλεπιδράσεις των σωματιδίων φτιάχνουν τον κόσμο, οπότε ο τρόπος με τον οποίο οι φυσικοί ελέγχουν την περιγραφή τους για τον κόσμο, είναι να συγκρίνουν τους τύπους πλάτους σκέδασης με τα αποτελέσματα των συγκρούσεων των σωματιδίων σε επιταχυντές όπως ο Μεγάλος Επιταχυντής Αδρονίων.
Κανονικά, για να υπολογίσουν τα πλάτη, οι φυσικοί υπολογίζουν συστηματικά όλους τους πιθανούς τρόπους, με τους οποίους οι συγκρουόμενοι κυματισμοί ενδέχεται να αντηχούν διαμέσου των κβαντικών πεδίων που διαποτίζουν το σύμπαν, προτού παράξουν τα σταθερά σωματίδια που κινούνται μακριά από το σημείο σύγκρουσης. Περιέργως, οι υπολογισμοί που περιλαμβάνουν εκατοντάδες σελίδες άλγεβρας συχνά αποδίδουν, στο τέλος, έναν τύπο μιας γραμμής.
Οι amplitudeologists (πλατολόγοι) υποστηρίζουν ότι η εικόνα του πεδίου αποκρύβει απλούστερα μαθηματικά πρότυπα. Ο Arkani-Hamed, που ηγείται της της προσπάθειας, χαρακτήρισε τα κβαντικά πεδία «μια βολική φαντασία». «Στη φυσική πολύ συχνά μπαίνουμε σε ένα λάθος δίνοντας σάρκα και οστά σε έναν φορμαλισμό», είπε. «Αρχίζουμε τα ολισθήματα στη γλώσσα λέγοντας ότι τα κβαντικά πεδία είναι πραγματικά, και τα σωματίδια είναι διεγέρσεις. Μιλάμε για εικονικά σωματίδια κι όλα αυτά τα πράγματα – που όμως δεν κάνουν κλικ, κλικ, κλικ στον ανιχνευτή κανενός. »
Οι amplitudeologists (πλατολόγοι) πιστεύουν ότι υπάρχει μια μαθηματικά απλούστερη και πιο αληθινή εικόνα για τις αλληλεπιδράσεις των σωματιδίων. Σε ορισμένες περιπτώσεις, διαπιστώνουν ότι η προοπτική της θεωρίας ομάδων του Wigner για τα σωματίδια μπορεί να επεκταθεί ώστε να περιγράψει και τις αλληλεπιδράσεις τους, χωρίς καμία από τις συνηθισμένες ασυναρτησίες των κβαντικών πεδίων.
Ο Lance Dixon, ένας διακεκριμένος πλατολόγος στον επιταχυντή SLAC, εξήγησε ότι οι ερευνητές έχουν χρησιμοποιήσει τις περιστροφές Poincaré που μελετήθηκαν από τον Wigner για να υπολογίσουν άμεσα το «πλάτος τριών σημείων» – έναν τύπο που περιγράφει ένα σωματίδιο που διασπάται σε δύο σωματίδια. Έχουν δείξει επίσης ότι τα πλάτη τριών σημείων χρησιμεύουν ως δομικά στοιχεία των πλατών τεσσάρων και πλέον σημείων, που περιλαμβάνουν όλο και περισσότερα σωματίδια. Αυτές οι δυναμικές αλληλεπιδράσεις φαίνονται να οικοδομούνται εξ’ αρχής από τις βασικές συμμετρίες.
«Το πιο ωραίο», σύμφωνα με τον Dixon, είναι ότι τα πλάτη σκέδασης που εμπλέκουν τα βαρυτόνια, οι υποτιθέμενοι φορείς της βαρυτικής δύναμης, αποδεικνύεται ότι είναι το τετράγωνο πλάτους που περιλαμβάνει γλοιόνια, τα σωματίδια που συνδέουν μεταξύ τους τα κουάρκ. Η βαρύτητα συνδέεται με το ίδιο το ύφασμα του χωροχρόνου, ενώ τα γλοιόνια κινούνται στο χωροχρόνο. Ωστόσο, τα βαρυτόνια και τα γλοιόνια προέρχονται φαινομενικά από τις ίδιες συμμετρίες. «Αυτό είναι πολύ περίεργο και φυσικά δεν είναι ακόμα κατανοητό με ποσοτική λεπτομέρεια, επειδή οι εικόνες είναι τόσο διαφορετικές», λέει ο Dixon.
Ο Arkani-Hamed και οι συνεργάτες του, εν τω μεταξύ, έχουν βρει εντελώς νέες μαθηματικές «διατάξεις» που φτάνουν απευθείας στην απάντηση, όπως το amplituhedron (πλατύεδρο) – ένα γεωμετρικό αντικείμενο που κωδικοποιεί πλάτη σκέδασης σωματιδίων στον όγκο του. Διώχνει την εικόνα των σωματιδίων που συγκρούονται στο χωροχρόνο και προκαλούν αλυσιδωτές αντιδράσεις αιτίας και αποτελέσματος. «Προσπαθούμε να βρούμε αυτά τα αντικείμενα εκεί έξω στον πλατωνικό κόσμο των ιδεών, που μας δίνουν τις [αιτιώδεις] ιδιότητες αυτόματα», δήλωσε ο Arkani-Hamed. «Τότε θα μπορούμε να πούμε, Αχα, τώρα μπορώ να δω γιατί αυτή η εικόνα μπορεί να ερμηνευθεί ως εξέλιξη.»
Νίμα Αρκάνι-Χαμέντ
Το «It-from-qubit (Είναι από κβαντοδυφία)» και η amplitudeology (πλατολογία) προσεγγίζουν τα μεγάλα ερωτήματα τόσο διαφορετικά που είναι δύσκολο να πούμε αν αυτές οι δύο εικόνες αλληλοσυμπληρώνονται ή έρχονται σε αντίθεση μεταξύ τους.
Σύμφωνα με την Netta Engelhardt, μια πιο σύνθετη διατύπωση της ερώτησης του τίτλου, «Τι είναι ένα σωματίδιο;» τίθεται ως «Ποια είναι τα θεμελιώδη δομικά στοιχεία του σύμπαντος στις πιο θεμελιώδεις του κλίμακες;»
Και μέχρι να βρεθεί μια πλήρης κβαντική θεωρία της βαρύτητας και του χωροχρόνου, η σύντομη απάντηση είναι: «Δεν γνωρίζουμε».
διαβάστε περισσότερες λεπτομέρειες στο άρθρο της Natalie Wolchover, «What Is a Particle?» στο Quantamagazine
Μεταφραση επιμέλεια
Σχόλια
Δημοσίευση σχολίου