Τα μαθηματικά της πανδημίας
του Σ. Τιτσώνη
Το μοντέλο SIR είναι ένα από τα απλούστερα μοντέλα ερμηνείας και πρόβλεψης επιδημιών και πολλά μοντέλα προκύπτουν από αυτή τη βασική μορφή. Αυτό το μοντέλο είναι ικανοποιητικά εφαρμόσιμο για μολυσματικές ασθένειες οι οποίες μεταδίδονται από τον άνθρωπο στον άνθρωπο και όπου η ανάρρωση προϋποθέτει μια διαρκή αντίσταση του οργανισμού, όπως στις μέρες μας ο ιός Covid-19.Ένα επιδημιολογικό μοντέλο (ΕΜ) εξετάζει και αξιοποιεί με μαθηματική μοντελοποίηση τον ρόλο που διαδραματίζει ένα μολυσμένο άτομο που ανήκει σε ένα σύνολο, για να προβλεφθεί η συμπεριφορά της εξάπλωσης ενός ιού μέσω του πληθυσμού.
Επειδή ο ασφαλέστερος τρόπος θα ήταν μια πειραματική διαδικασία πάνω σε ανθρώπινους πληθυσμούς και κάτι τέτοιο (στα κράτη δικαίου. . .) εκτός από αδύνατο είναι και ανήθικο, οι πληροφορίες που αξιοποιούνται προέρχονται από ιστορικά δεδομένα, ιατρικά στοιχεία, επιστημονικές αναλύσεις που μοντελοποιούνται μέσω προσομοιώσεων σε ηλεκτρονικούς υπολογιστές.
Τα ΕΜ εφαρμόζονται για να εισπραχθούν ποσοτικές και ποιοτικές πληροφορίες για την εξέλιξη μιας επιδημίας, τον έλεγχό της και την προσπάθεια ελέγχου της μετάδοσης ενός ιού.
Συνήθως, χρησιμοποιούνται οι συμβολισμοί με S (Susceptible) για την κατηγορία των ατόμων που είναι ευάλωτα, I (Infectious) για την κατηγορία των μολυσμένων ατόμων (που έχουν προσβληθεί από τον ιό και μπορούν να τον μεταδώσουν), R (recovery) την κατηγορία των ατόμων που έχουν μεν μολυνθεί αλλά δεν μεταδίδουν τον ιό (είναι άνοσα ή έχουν αποκτήσει ανοσία, έχουν μπει σε καραντίνα, ή έχουν πεθάνει) και Ε τα άτομα που έχουν τον ιό σε φάση επώασης (incubation).
Τέτοια μοντέλα είναι τα SIS, SIR, SIRS, SSIR κ.λπ. με την διαδοχή των γραμμάτων να ερμηνεύουν την πορεία εξέλιξης της εξάπλωσης ενός ιού. Π.χ για το μοντέλο SIR (Kermack – McKendrick) που είναι ένα χαρακτηριστικό μοντέλο στο οποίο και αναφερόμαστε πιο κάτω, η διαδοχή SIR σημαίνει:
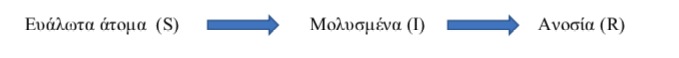
(Λίγα μαθηματικά που μπορούν να παρακάμψουν όσοι δεν ενδιαφέρονται: Επειδή τα S, Ι, R είναι ποσότητες που εξαρτώνται από τον χρόνο, εκφράζονται ως συναρτήσεις του χρόνου t, δηλ. S (t), I (t), R (t).
Οι διαφορικές εξισώσεις που περιγράφουν το μοντέλο είναι:
dS/dt = – β S I/Ν
dI/dt = β S I/Ν – γ I
dR/dt = γ I
με β και γ θετικούς σταθερούς αριθμούς, όπου β είναι ο μέσος αριθμός επαφών ανά άτομο σε μια μονάδα χρόνου (π.χ. μια μέρα), πολλαπλασιασμένος επί την πιθανότητα μετάδοσης του ιού σε μια επαφή μεταξύ ενός ευάλωτου και ενός μολυσμένου ατόμου. Επίσης γ είναι ο λόγος των άνοσων πλέον ή πεθαμένων (θεωρούνται μακάβρια άνοσοι!) σε μια μέρα προς τον ολικό αριθμό των μολυσμένων την ίδια μέρα.
Αν η διάρκεια της λοίμωξης είναι D, τότε γ = 1/D, αφού ένα άτομο ανακάμπτει σε D μονάδες χρόνου.
Ακόμη S(t) + I(t) + R(t) = N
όπου Ν είναι ο αριθμός του πληθυσμού.
Αρχικές συνθήκες: Για t = 0 είναι R = 0 (δηλαδή σε χρόνο 0, Άνοσοι (R) = 0 και S(0) + I(0) = N (δηλαδή σε χρόνο 0 το άθροισμα των Ευάλωτων (S) και των Μολυσμένων (Ι) ισούται με τον αρχικό πληθυσμό.
Είναι περιττό να αναφέρω τη λύση του συστήματος των διαφορικών εξισώσεων-υπάρχει άλλωστε σε πολλά sites-. Έκανα απλώς αυτή την αναφορά για να δώσω την ευκαιρία να εξοικειωθούν κάποιοι με την ορολογία των ημερών.)











Σχόλια
Δημοσίευση σχολίου