Richard Feynman: Η διατήρηση της ενέργειας
«…. Η διατήρηση της ενέργειας είναι δυσκολονόητη …. Θα ήθελα να χρησιμοποιήσω μια όχι και τόσο έξυπνη αναλογία για να (την) εξηγήσω …
Φανταστείτε ότι μια μητέρα αφήνει το παδί της μόνο, σ’ ένα δωμάτιο με 28 κύβους από εντελώς άφθαρτη ύλη. Το παδί παίζει με τους κύβους όλη την ημέρα. Όταν επιστρέφει η μητέρα του, βρίσκει ότι οι κύβοι είναι ακόμη 28. Κάθε φορά ελέγχει μήπως χάθηκε κανένας. Αυτό συνεχίζεται για μερικές μέρες.
Ξαφνικά, επιστρέφοντας μια μέρα, διαπιστώνει πως οι κύβοι είναι 27. Βρίσκει όμως έναν έξω από το παράθυρο όπου τον είχε πετάξει το παιδί.
Το πρώτο πράγμα που πρέπει να λάβει υπ’ όψη του κανείς όταν πρόκειται για νόμους διατήρησης, είναι ότι αυτό που προσπαθεί να ελέγξει, δεν διαφεύγει από κάπου. Το ίδιο θα μπορούσε να συμβεί με τον αντίθετο ακριβώς τρόπο, αν δηλαδή ένα άλλο παιδί ερχόταν να παίξει με το παιδί στο δωμάτιο φέρνοντας μαζί του μερικούς κύβους. Είναι φανερό ότι τέτοια ζητήματα πρέπει να λάβει κανείς υπ’ όψη του όταν μελετά τους νόμους διατήρησης. Ας υποθέσουμε ότι κάποια μέρα μπαίνει η μητέρα στο δωμάτιο, μετρά τους κύβους και τους βρίσκει μόνο 25.
Υποψιάζεται, ωστόσο, ότι το παιδί έχει κρύψει τους άλλους τρεις μέσα σ’ ένα κουτί παιχνιδιών.
Του λέει λοιπόν: «Θ’ ανοίξω το κουτί». «Όχι», της λέει το παιδί, «δεν μπορείς να το αγγίξεις».
H μητέρα του όμως είναι πολύ έξυπνη και του απαντά: «Ξέρω ότι το κουτί ζυγίζει άδειο 16 ουγγιές και ότι κάθε κύβος ζυγίζει 3 ουγγιές. Δεν έχω, λοιπόν, παρά να ζυγίσω το κουτί». Έτσι ο συνολικός αριθμός των κύβων θα είναι:
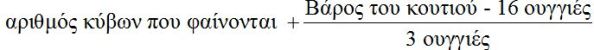
και αυτό ισούται με 28. Προς στιγμήν η μέθοδος αποδίδει. Κάποια μέρα όμως το εν λόγω άθροισμα δεν δίνει τη σωστή τιμή. Τότε η μητέρα παρατηρεί πως η στάθμη του βρώμικου νερού στο νεροχύτη έχει αλλάξει. Ξέρει ότι το βάθος του νερού είναι 6 ίντσες όταν δεν υπάρχει μέσα κάποιος κύβος και ότι θα ανέβαινε κατά το ¼ της ίντσας αν βρισκόταν μέσα ένας κύβος. Προσθέτει, λοιπόν, στο άθροισμα ένα ακόμη όρο και έχει τώρα:
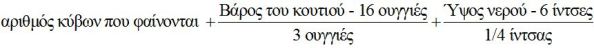
oπότε παίρνει και πάλι 28. Όσο το αγόρι σκαρφίζεται διάφορα κόλπα και η μητέρα του συνεχίζει να είναι εξ’ ίσου εφευρετική, προστίθενται όλο και περισσότεροι όροι που αντιπροσωπεύουν κύβους.
Ωστόσο, από μαθηματική άποψη πρόκειται για αφηρημένους υπολογισμούς, αφού οι κύβοι δεν φαίνονται.
Ας υποθέσουμε κατ’ αρχάς ότι σε καμιά από τις παραπάνω περιπτώσεις δεν είχαμε δει ποτέ τους κύβους. Ο όρος «αριθμός των κύβων που φαίνονται» δεν θα υπήρχε. Στην περίπτωση αυτή, η μητέρα θα έπρεπε να κάνει πάντοτε υπολογισμούς μ’ ένα σωρό όρους, όπως «κύβοι στο κουτί», «κύβοι στο νερό» κ.τ.λ.
Με την ενέργεια συμβαίνει αυτή ακριβώς η διαφορά: δεν υπάρχουν «κύβοι», όσο τουλάχιστον ξέρουμε. Σε αντίθεση επίσης με την περίπτωση των κύβων, στην ενέργεια δεν προκύπτουν ακέραιοι αριθμοί. Αυτό για την ταλαίπωρη σημαίνει πως, υπολογίζοντας έναν όρο ίσως βρει 61/8 κύβους, ενώ υπολογίζοντας κάποιον άλλο ίσως πάρει 7/8 του κύβου, οπότε οι άλλοι όροι θα δώσουν 21, για να είναι το σύνολο 28. Ακριβώς έτσι γίνεται με την ενέργεια.
Για την ενέργεια έχουμε ανακαλύψει ένα νοητικό σχήμα με μια σειρά κανόνων. Για κάθε διαφορετικό είδος ενέργειας μπορούμε να υπολογίσουμε έναν αριθμό, εφαρμόζοντας ένα διαφορετικό σύνολο κανόνων.
Όταν προσθέτουμε έναν όλους τους αριθμούς που αντιπροσωπεύουν διαφορετικές μορφές ενέργειας, παίρνουμε κάθε στιγμή την ίδια τιμή του αθροίσματος με την αρχική.
Όσο ξέρουμε όμως, δεν υπάρχουν ακέραιες ποσότητες, μικροί «κύβοι». Είναι μια αφηρημένη, καθαρά μαθηματική διαδικασία: υπάρχει ένας αριθμός που δεν αλλάζει, οποιαδήποτε στιγμή κι αν τον υπολογίσουμε.
Δεν μπορώ να το εξηγήσω καλύτερα απ’ ότι προσπάθησα…»
Richard Feynman: «Ο χαρακτήρας του φυσικού κόσμου>>
Φανταστείτε ότι μια μητέρα αφήνει το παδί της μόνο, σ’ ένα δωμάτιο με 28 κύβους από εντελώς άφθαρτη ύλη. Το παδί παίζει με τους κύβους όλη την ημέρα. Όταν επιστρέφει η μητέρα του, βρίσκει ότι οι κύβοι είναι ακόμη 28. Κάθε φορά ελέγχει μήπως χάθηκε κανένας. Αυτό συνεχίζεται για μερικές μέρες.
Ξαφνικά, επιστρέφοντας μια μέρα, διαπιστώνει πως οι κύβοι είναι 27. Βρίσκει όμως έναν έξω από το παράθυρο όπου τον είχε πετάξει το παιδί.
Το πρώτο πράγμα που πρέπει να λάβει υπ’ όψη του κανείς όταν πρόκειται για νόμους διατήρησης, είναι ότι αυτό που προσπαθεί να ελέγξει, δεν διαφεύγει από κάπου. Το ίδιο θα μπορούσε να συμβεί με τον αντίθετο ακριβώς τρόπο, αν δηλαδή ένα άλλο παιδί ερχόταν να παίξει με το παιδί στο δωμάτιο φέρνοντας μαζί του μερικούς κύβους. Είναι φανερό ότι τέτοια ζητήματα πρέπει να λάβει κανείς υπ’ όψη του όταν μελετά τους νόμους διατήρησης. Ας υποθέσουμε ότι κάποια μέρα μπαίνει η μητέρα στο δωμάτιο, μετρά τους κύβους και τους βρίσκει μόνο 25.
Υποψιάζεται, ωστόσο, ότι το παιδί έχει κρύψει τους άλλους τρεις μέσα σ’ ένα κουτί παιχνιδιών.
Του λέει λοιπόν: «Θ’ ανοίξω το κουτί». «Όχι», της λέει το παιδί, «δεν μπορείς να το αγγίξεις».
H μητέρα του όμως είναι πολύ έξυπνη και του απαντά: «Ξέρω ότι το κουτί ζυγίζει άδειο 16 ουγγιές και ότι κάθε κύβος ζυγίζει 3 ουγγιές. Δεν έχω, λοιπόν, παρά να ζυγίσω το κουτί». Έτσι ο συνολικός αριθμός των κύβων θα είναι:
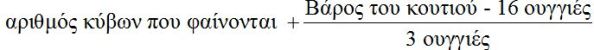
και αυτό ισούται με 28. Προς στιγμήν η μέθοδος αποδίδει. Κάποια μέρα όμως το εν λόγω άθροισμα δεν δίνει τη σωστή τιμή. Τότε η μητέρα παρατηρεί πως η στάθμη του βρώμικου νερού στο νεροχύτη έχει αλλάξει. Ξέρει ότι το βάθος του νερού είναι 6 ίντσες όταν δεν υπάρχει μέσα κάποιος κύβος και ότι θα ανέβαινε κατά το ¼ της ίντσας αν βρισκόταν μέσα ένας κύβος. Προσθέτει, λοιπόν, στο άθροισμα ένα ακόμη όρο και έχει τώρα:
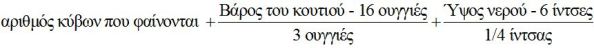
oπότε παίρνει και πάλι 28. Όσο το αγόρι σκαρφίζεται διάφορα κόλπα και η μητέρα του συνεχίζει να είναι εξ’ ίσου εφευρετική, προστίθενται όλο και περισσότεροι όροι που αντιπροσωπεύουν κύβους.
Ωστόσο, από μαθηματική άποψη πρόκειται για αφηρημένους υπολογισμούς, αφού οι κύβοι δεν φαίνονται.
Ας υποθέσουμε κατ’ αρχάς ότι σε καμιά από τις παραπάνω περιπτώσεις δεν είχαμε δει ποτέ τους κύβους. Ο όρος «αριθμός των κύβων που φαίνονται» δεν θα υπήρχε. Στην περίπτωση αυτή, η μητέρα θα έπρεπε να κάνει πάντοτε υπολογισμούς μ’ ένα σωρό όρους, όπως «κύβοι στο κουτί», «κύβοι στο νερό» κ.τ.λ.
Με την ενέργεια συμβαίνει αυτή ακριβώς η διαφορά: δεν υπάρχουν «κύβοι», όσο τουλάχιστον ξέρουμε. Σε αντίθεση επίσης με την περίπτωση των κύβων, στην ενέργεια δεν προκύπτουν ακέραιοι αριθμοί. Αυτό για την ταλαίπωρη σημαίνει πως, υπολογίζοντας έναν όρο ίσως βρει 61/8 κύβους, ενώ υπολογίζοντας κάποιον άλλο ίσως πάρει 7/8 του κύβου, οπότε οι άλλοι όροι θα δώσουν 21, για να είναι το σύνολο 28. Ακριβώς έτσι γίνεται με την ενέργεια.
Για την ενέργεια έχουμε ανακαλύψει ένα νοητικό σχήμα με μια σειρά κανόνων. Για κάθε διαφορετικό είδος ενέργειας μπορούμε να υπολογίσουμε έναν αριθμό, εφαρμόζοντας ένα διαφορετικό σύνολο κανόνων.
Όταν προσθέτουμε έναν όλους τους αριθμούς που αντιπροσωπεύουν διαφορετικές μορφές ενέργειας, παίρνουμε κάθε στιγμή την ίδια τιμή του αθροίσματος με την αρχική.
Όσο ξέρουμε όμως, δεν υπάρχουν ακέραιες ποσότητες, μικροί «κύβοι». Είναι μια αφηρημένη, καθαρά μαθηματική διαδικασία: υπάρχει ένας αριθμός που δεν αλλάζει, οποιαδήποτε στιγμή κι αν τον υπολογίσουμε.
Δεν μπορώ να το εξηγήσω καλύτερα απ’ ότι προσπάθησα…»
Richard Feynman: «Ο χαρακτήρας του φυσικού κόσμου>>











Σχόλια
Δημοσίευση σχολίου