Κοινωνική απόσταση και τριγωνικά πλέγματα
 |
| Photo by Shaun Meintjes on Unsplash |
Η πανδημία του κορωνοϊού, εκτός από τις γνωστές καταστροφικές της συνέπειες, έχει ενεργοποιήσει με εντυπωσιακό τρόπο την ανάγκη των ανθρώπων να παραμένουν πνευματικά ενεργοί. Δεκάδες κείμενα, μεταδόσεις και αναρτήσεις επιχειρούν να κρατήσουν ζωντανό το ενδιαφέρον μας για την τέχνη, την επιστήμη και τη γνώση. Σε αυτό το πνεύμα, το διαδικτυακό επιστημονικό περιοδικό + Plus δημοσιεύει μακροσκελή άρθρα με επιστημονικό περιεχόμενο άλλα και μικρότερα κείμενα που επιχειρούν να συνδέσουν τη δύσκολη συγκυρία με τη γνώση και την ψυχαγωγία.Σε ένα από αυτά τα κείμενα, στην ενότητα Maths in a minute, παρουσιάζεται μια μορφή μαθηματικής οργάνωσης της απόστασης που πρέπει να διατηρήσει μια ομάδα ανθρώπων που έχει βγει βόλτα στο πάρκο για να χαρεί τον ανοιξιάτικο ήλιο.
Η ανάρτηση δεν αποτελεί κάποια αυστηρή παρουσίαση του τρόπου οργάνωσης της απόστασης μεταξύ των ανθρώπων στο δημόσιο χώρο αυτή την εποχή. Η προσέγγιση του δημοσιεύματος θα μπορούσε να χαρακτηριστεί στατική και μη ρεαλιστική, αφού δεν λαμβάνει υπόψιν αρκετούς παράγοντες (κίνηση, χρόνο, φυσικά εμπόδια κ.ά) που αφορούν την παρουσία των ανθρώπων σε ένα πάρκο. Παρ ’όλα αυτά, αναδεικνύει με απλό τρόπο τη δυνατότητα των μαθηματικών να προσεγγίζουν δεκάδες ζητήματα της καθημερινότητάς μας και να αναζητούν λύσεις για αυτά.
«Φανταστείτε αρκετούς ανθρώπους σε ένα πάρκο να απολαμβάνουν τον ήλιο», γράφει η Marianne Freiberger στο κείμενό της στο περιοδικό. Και συνεχίζει: «Κάθε άτομο θέλει να διατηρήσει τουλάχιστον δύο μέτρα απόσταση από όλους τους άλλους, και όλοι θέλουν να έχουν γύρω τους, στην ελάχιστη απόσταση των δύο μέτρων, όσο το δυνατόν περισσότερα άτομα. Ποιες θέσεις πρέπει να λάβουν για να συμβεί αυτό; Και ποιος είναι ο αριθμός των ατόμων που θα έχει κάποιος σε απόσταση δύο μέτρων ύστερα από αυτή τη διευθέτηση;
» Ας ξεκινήσουμε με ένα άτομο που θα το ονομάσουμε Α. Όσοι θέλουν να απέχουν δύο μέτρα από το άτομο Α πρέπει να τοποθετηθούν στο σημείο ενός κύκλου που έχει το Α στο κέντρο του σε μια ακτίνα δύο μέτρων. Ας παρατηρήσουμε δύο ακόμα άτομα σε αυτόν τον κύκλο, το άτομο B και το άτομο C. Δεδομένου ότι τα άτομα B και C θέλουν, επίσης, να απέχουν δύο μέτρα το ένα από το άλλο, το τρίγωνο που σχηματίζεται από τις θέσεις των ατόμων A, B και C πρέπει να είναι ένα ισόπλευρο τρίγωνο με μήκος πλευρών το 2.
»Πόσα τέτοιου είδους τρίγωνα μπορούν να χωρέσουν γύρω από το άτομο Α και να μην επικαλύπτονται; Οι γωνίες σε ένα ισόπλευρο τρίγωνο είναι όλες ίσες με 60 μοίρες. Συνολικά, υπάρχουν 360 μοίρες διαθέσιμες γύρω από το άτομο Α, πράγμα που σημαίνει ότι γύρω από τη θέση του ατόμου Α μπορούν να χωρέσουν έξι ισόπλευρα τρίγωνα (360/60 = 6). Με άλλα λόγια, τα πρόσωπα που μπορούν να τοποθετηθούν σε δύο μέτρα απόσταση από το άτομο Α και αυτά να απέχουν επίσης δύο μέτρα το καθένα από τα δύο γειτονικά τους πρόσωπα στον κύκλο είναι έξι.
»Το ίδιο ισχύει και για κάθε άλλο πρόσωπο που βρίσκεται στον κύκλο του Α. Ο αριθμός των πλησιέστερων γειτόνων του, σε απόσταση δύο μέτρων, είναι έξι, τα οποία θα πρέπει να αναπτυχθούν γύρω και από αυτό το άτομο σε μια διάταξη που θα έχει το σχήμα ενός κανονικού εξαγώνου και θα αποτελείται από έξι ισόπλευρα τρίγωνα.

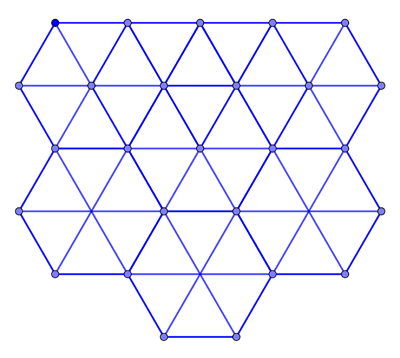
»Δεδομένου ότι αυτό ισχύει για κάθε άτομο, η απάντηση είναι ότι οι άνθρωποι στο πάρκο θα πρέπει να αναπτυχθούν σε ένα τριγωνικό πλέγμα που θα αποτελείται από ισόπλευρα τρίγωνα. Κάθε άτομο στο πλέγμα θα βρίσκεται, επίσης, στο κέντρο ενός κανονικού εξαγώνου».
Πηγή:https://plus.maths.org/content/













Σχόλια
Δημοσίευση σχολίου